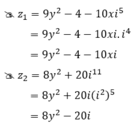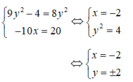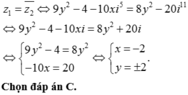81x2 - 6yz -9y2-z2

Những câu hỏi liên quan
Phân tích các đa thức thành nhân tử
a)6x3y2.(2-x)+9x2y2.(x-2)
b)x2-4x+4y-y2
c)81x2+6yz-9y2-z2
\(a.6x^3y^2.\left(2-x\right)+9x^2y^2.\left(x-2\right)\\ =6x^3y^2.\left(2-x\right)-9x^2y^2.\left(2-x\right)\\ =3x^2y^2\left(2-x\right)\left(2x-3\right)\)
Đúng 2
Bình luận (0)
Lời giải:
a.
$=6x^3y^2(2-x)-9x^2y^2(2-x)$
$=(2-x)(6x^3y^2-9x^2y^2)$
$=(2-x).3x^2y^2(2x-3)=3x^2y^2(2-x)(2x-3)$
b.
$=(x^2-y^2)-(4x-4y)=(x-y)(x+y)-4(x-y)$
$=(x-y)(x+y-4)$
c.
$81x^2-(9y^2-6yz+z^2)$
$=(9x)^2-(3y-z)^2=(9x-3y+z)(9x+3y-z)$
Đúng 2
Bình luận (0)
a) m2 - n2 b) 4m2-16n2 c) 49 - 16x2 d) 25 - 9y2 e) 81x2-16y2
a, \(m^2-n^2=\left(m-n\right)\left(m+n\right)\)
b, \(4m^2-16n^2=\left(2m-4n\right)\left(2m+4n\right)=4\left(m-2n\right)\left(m+2n\right)\)
c, \(49-16x^2=\left(7-4x\right)\left(7+4x\right)\)
d, \(25-9y^2=\left(5-3y\right)\left(5+3y\right)\)
e, \(81x^2-16y^2=\left(9x-4y\right)\left(9x+4y\right)\)
Đúng 1
Bình luận (0)
Tìm số thực x,y để hai số phức z1 9y2 - 4 - 10xi5 và z2 8y2 + 20i11 là liên hợp của nhau?
z
1
9
y
2
-
4
-
10
x
i
5
v
à
z
2
8
y
2...
Đọc tiếp
Tìm số thực x,y để hai số phức z1 = 9y2 - 4 - 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau? z 1 = 9 y 2 - 4 - 10 x i 5 v à z 2 = 8 y 2 + 20 i 11 l à
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Tìm x,y,z thoả mãn: 2x2+9y2+z2+6x(1-y)-8z+25=0
\(\Leftrightarrow\left(x^2-6xy+9y^2\right)+\left(x^2+6x+9\right)+\left(z^2-8z+16\right)=0\)
\(\Leftrightarrow\left(x-3y\right)^2+\left(x+3\right)^2+\left(z-4\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3y=0\\x+3=0\\z-4=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-1\\z=4\end{matrix}\right.\)
Đúng 3
Bình luận (0)
phân tích đa thức thành nhân tử
a, 4x2-9y2+6x-9y
b, 1-2x+2yz+x2-y2-z2
a) \(4x^2-9y^2+6x-9y\)
\(=\left(2x-3y\right)\left(2x+3y\right)+3\left(2x-3y\right)\)
\(=\left(2x-3y\right)\left(2x+3y+3\right)\)
b) \(1-2x+2yz+x^2-y^2-z^2\)
\(=\left(x^2-2x+1\right)-\left(y^2-2yz+z^2\right)\)
\(=\left(x-1\right)^2-\left(y-z\right)^2\)
\(=\left(x-y+z-1\right)\left(x+y-z-1\right)\)
Tick hộ mình nha 😘
Đúng 5
Bình luận (0)
Tìm số thực x; y để hai số phức z1 9y2 – 4 – 10xi5 và z2 8y2 + 20i11 là liên hợp của nhau? A. x -2; y 2. B. x 2; y ±2. C. x 2; y 2. D. x -2; y ±2.
Đọc tiếp
Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Chọn D.
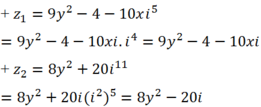
+ z1 và z2 là liên hợp của nhau khi và chỉ khi:
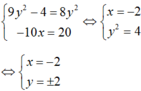
Đúng 0
Bình luận (0)
Tìm tất cả các số thực x, y để hai số phức
z
1
9
y
2
-
4
-
10
x
i
5
,
z
2
8
y
2
+
10
i
11
là hai số phức liên hợp của nhau. A.
x...
Đọc tiếp
Tìm tất cả các số thực x, y để hai số phức z 1 = 9 y 2 - 4 - 10 x i 5 , z 2 = 8 y 2 + 10 i 11 là hai số phức liên hợp của nhau.
A. x = 2 y = ± 2
B. x = ± 2 y = 2
C. x = - 2 y = ± 2
D. x = - 2 y = 2
Tìm tọa độ tâm và bán kính mặt cầu sau đây:
a) x2+y2+z2-8x+2y+1=0
b) 3x2+3y2+3z2+6x-3y+15z-2=0
c) 9x2+9y2+9z2-6x+18y+1=0
a/ \(x^2-2.4x+16+y^2+2y+1+z^2=16\Leftrightarrow\left(x-4\right)^2+\left(y+1\right)^2+z^2=16\)
\(\Rightarrow\left\{{}\begin{matrix}I\left(4;-1;0\right)\\R=\sqrt{16}=4\end{matrix}\right.\)
b/ \(x^2+y^2+z^2+2x-y+5z-\dfrac{2}{3}=0\Leftrightarrow x^2+2x+1+y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+z^2+2.\dfrac{5}{2}z+\dfrac{25}{4}=\dfrac{2}{3}+1+\dfrac{1}{4}+\dfrac{25}{4}\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-\dfrac{1}{2}\right)^2+\left(z+\dfrac{5}{2}\right)^2=\dfrac{49}{6}\) \(\Rightarrow\left\{{}\begin{matrix}I\left(-1;\dfrac{1}{2};-\dfrac{5}{2}\right)\\R=\dfrac{7}{\sqrt{6}}\end{matrix}\right.\)
P/s: câu c bạn tự làm nốt ạ!
Đúng 3
Bình luận (0)
trả lời cho nguyễn hồng hạnh pro x2 + -4 0Sắp xếp lại các điều khoản:-4 + 81x2 0Giải quyết-4 + 81x2 0Giải quyết cho biến x.Di chuyển tất cả các điều khoản có chứa x sang bên trái, tất cả các điều khoản khác về bên phải.Thêm 4 vào mỗi bên của phương trình.-4 + 4 + 81x2 0 + 4Kết hợp các điều khoản như: -4 + 4 00 + 81x2 0 + 481x2 0 + 4Kết hợp như các điều khoản: 0 + 4 481x2 4Chia mỗi bên 81.x2 0,04938271605Đơn giản hóax2 0,04938271605Lấy căn bậc hai của mỗi bên:x {-,222222222, 0,2222222...
Đọc tiếp
trả lời cho nguyễn hồng hạnh pro
x2 + -4 = 0
Sắp xếp lại các điều khoản:
-4 + 81x2 = 0
Giải quyết
-4 + 81x2 = 0
Giải quyết cho biến 'x'.
Di chuyển tất cả các điều khoản có chứa x sang bên trái, tất cả các điều khoản khác về bên phải.
Thêm '4' vào mỗi bên của phương trình.
-4 + 4 + 81x2 = 0 + 4
Kết hợp các điều khoản như: -4 + 4 = 0
0 + 81x2 = 0 + 4
81x2 = 0 + 4
Kết hợp như các điều khoản: 0 + 4 = 4
81x2 = 4
Chia mỗi bên '81'.
x2 = 0,04938271605
Đơn giản hóa
x2 = 0,04938271605
Lấy căn bậc hai của mỗi bên:
x = {-,222222222, 0,222222222}
81x2+8x5-7x(27-2)