Giải tự luận giúp em 1209 hoặc cả 2 câu thì càng tốt ạ

Những câu hỏi liên quan
Cho tổng 2 số tự nhiên liên tiếp là 1017. Tìm 2 số tự nhiên đó
Mn giải giúp mk nhé, có cả câu lời giải thì càng tốt, mk sẽ tik
Mn giúp mk với ah, mk dg lm toán nâng cao
Đúng 0
Bình luận (0)
1018 , 1019 1020
giúp mình câu b ạ, cả câu c thì càng tốt
2: FK vuôg góc BE; AE vuông góc BE
=>FK//AE
Chứng minh tương tự, ta được AF//EK
=>AFKE là hbh
=>AF=EK
=>AF/EC=EK/EC
ΔCEK đồng dạng với ΔCAM
=>EK/EC=AM/AC
=>AF/EC=AM/AC
ΔAFB đồng dạng với ΔCEB
=>góc ABF=góc CBE
c: AM/AC=AF/EC=AB/BC
=>AM/AC=AB/BC
=>ΔAMB đồng dạng với ΔCAB
=>góc ABC=góc ABM
=>BA là phân giác của góc MBC
Đúng 0
Bình luận (0)
 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
Giải giúp mình ạ, làm được bao nhiêu câu cũng được ạ hết thì càng tốt ạ
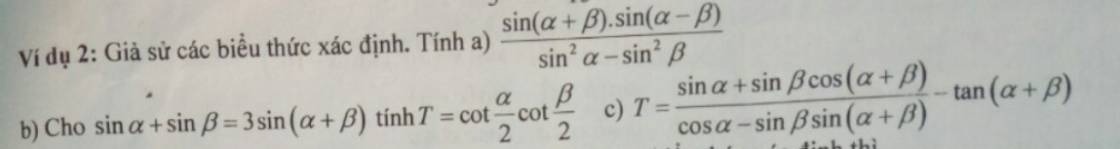
a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)
Đúng 0
Bình luận (0)
Mọi người giúp em những câu này với ạ, với có cả giải thích thì càng tốt, cần gấp ạComplete the sentences using the words in brackets without changing the original meaning. Do not change the words given1. The issue of the corona virus was so important that we could not ignore it (such)- The issue of the coronavirus was of...... consideration.2. He’s not likely to arrive before nightfall (chances)- The.....slim.3. In my opinion, I would be happy to employ the company next time. (hesitation)- If I...
Đọc tiếp
Mọi người giúp em những câu này với ạ, với có cả giải thích thì càng tốt, cần gấp ạ
Complete the sentences using the words in brackets without changing the original meaning. Do not change the words given
1. The issue of the corona virus was so important that we could not ignore it (such)
-> The issue of the coronavirus was of...... consideration.
2. He’s not likely to arrive before nightfall (chances)
-> The.....slim.
3. In my opinion, I would be happy to employ the company next time. (hesitation)
-> If I......the company next time.
4. This is the first time I’ve seen him panic. (head)
-> Never......before.
5. He was so angry that his face changed color. (go)
-> His.......face.
Complete the sentences using the words in brackets without changing the original meaning. Do not change the words given
1. The issue of the corona virus was so important that we could not ignore it (such)
-> The issue of the coronavirus was of...such importance that we could take it into... consideration.
2. He’s not likely to arrive before nightfall (chances)
-> The...chances of his arriving before nightfall are..slim.
3. In my opinion, I would be happy to employ the company next time. (hesitation)
-> If I...were to be asked, I would ...the company next time. (mình nghĩ là if I were to be asked, ko biết if I were you ở đây có dùng đc ko nhỉ)
4. This is the first time I’ve seen him panic. (head)
-> Never...have I seen him losing his head...before.
5. He was so angry that his face changed color. (go)
-> His.......face.
mấy câu trên mình cũng ko chắc lắm đâu -.- Còn câu 5 mới nghĩ ra đc idiom go up the wall = angry mà chưa biết ghép vào câu như nào nữa
Đúng 1
Bình luận (1)
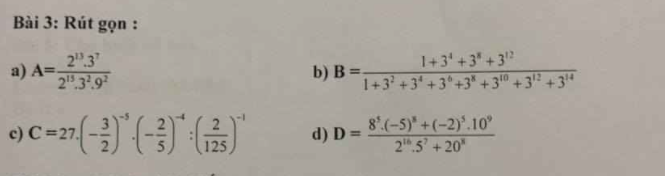 giúp mình với ạ cả 4 câu càng nhanh càng tốt
giúp mình với ạ cả 4 câu càng nhanh càng tốt
\(A=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^2\cdot9^2}=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^6}=\dfrac{3}{4}\)
\(C=27\cdot\left(-\dfrac{3}{2}\right)^{-5}\cdot\left(-\dfrac{2}{5}\right)^{-4}:\left(\dfrac{2}{125}\right)^{-1}\)
\(=27\cdot\dfrac{-32}{243}\cdot\dfrac{625}{16}\cdot\dfrac{2}{125}\)
\(=\dfrac{-32}{9}\cdot\dfrac{1}{8}\cdot5\)
\(=-\dfrac{20}{9}\)
Đúng 2
Bình luận (0)
Mọi người giúp em mấy câu này với ạ!! Một vài câu cũng được mà làm hết thì càng tốt

4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
Đúng 1
Bình luận (0)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
7.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-\left(x+1\right)+\left(x+1-\sqrt[3]{1+3x}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{1+2x}+x+1}+\dfrac{x^2\left(x+3\right)}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{1+2x}+x+1}+\dfrac{x+3}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{3}{1+1+1}=1\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+3\right)=3\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời

ai giải giúp em toàn bộ bài ở trên ảnh với, trình bày ra giúp em luôn thì càng tốt ạ, em đang cần gấp huhu 🥹
Bài 1:
a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)
= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\)
= \(\dfrac{20}{21}\)
b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)
= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)
= \(\dfrac{31}{84}\)
c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{3}{8}\)
Đúng 1
Bình luận (0)
d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{9}\)
e, {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))2 : 2 ] - 1}. \(\dfrac{4}{5}\)
= {[ (-\(\dfrac{1}{6}\))2 : 2] - 1}. \(\dfrac{4}{5}\)
= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)
= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)
=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)
= -\(\dfrac{71}{90}\)
Đúng 1
Bình luận (0)
g, [(\(\dfrac{32}{25}\) +1): \(\dfrac{2}{3}\)].(\(\dfrac{3}{4}\) - \(\dfrac{1}{8}\))2
= [ \(\dfrac{57}{25}\) : \(\dfrac{2}{3}\)].(\(\dfrac{5}{8}\))2
= \(\dfrac{171}{50}\). \(\dfrac{25}{64}\)
= \(\dfrac{171}{28}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
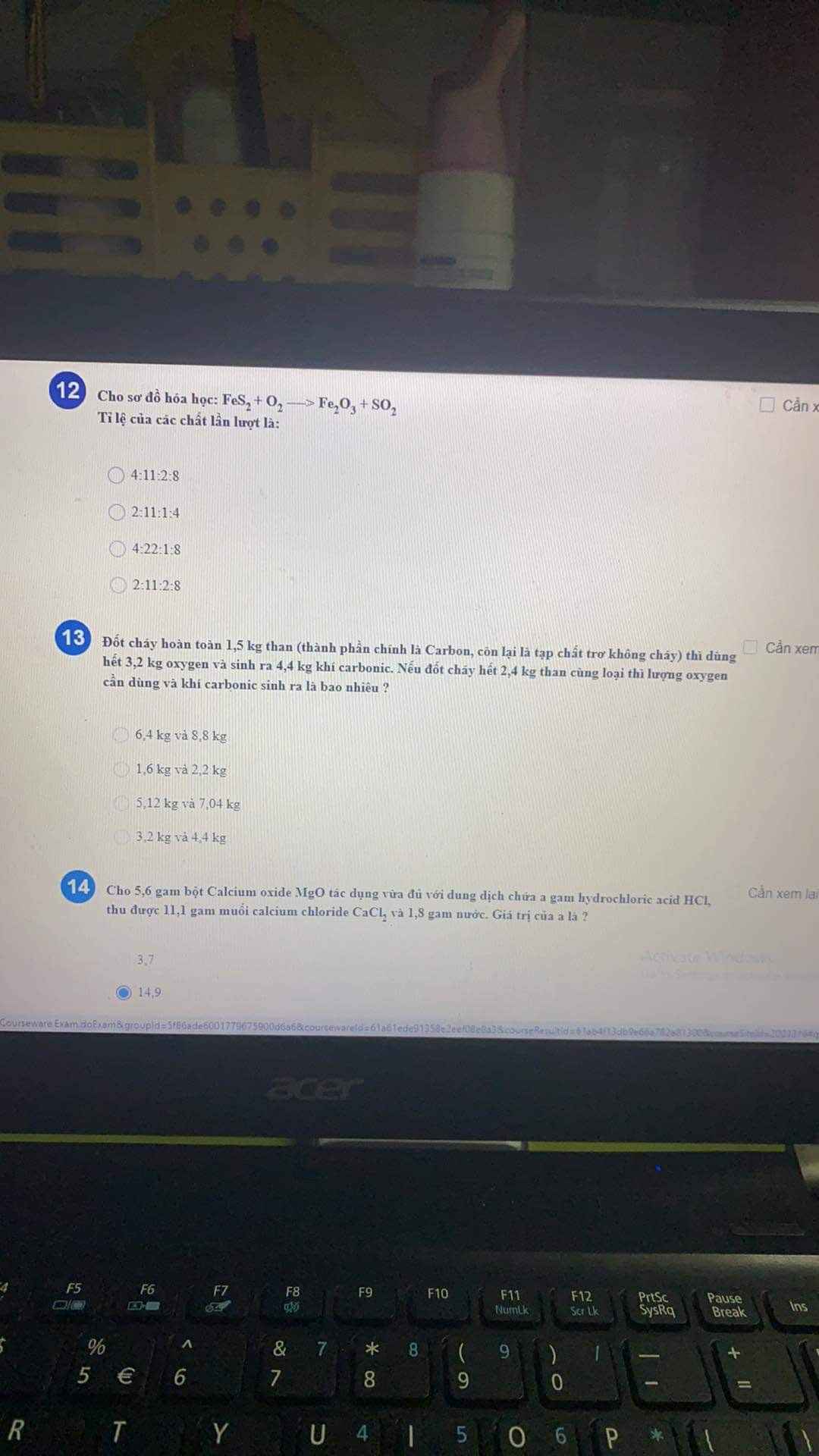
M.n giúp mk câu 13 với ạ, mk cảm ơn rất nhìu(có lời giải chi tiết thì càng tốt nka)

















