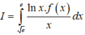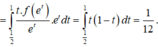2. x2-50
Phân tích làm sao cho ra là 0
Những câu hỏi liên quan
\(\sqrt{4x-3}\) - \(\sqrt{x2-3}\)
= 0
Em ra là 4x - x2 = 0, tới đây làm sao nữa ạ?
`\sqrt{4x-3}-\sqrt{x^2-3}=0` `ĐK: x >= \sqrt{3}`
`<=>\sqrt{4x-3}=\sqrt{x^2-3}`
`<=>4x-3=x^2-3`
`<=>x^2-4x=0`
`<=>x(x-4)=0`
`<=>[(x=0(ko t//m)),(x=4(t//m)):}`
Vậy `S={4}`.
Đúng 2
Bình luận (1)
Một học sinh làm bài tích phân
I
∫
0
1
d
x
1
+
x
2
theo các bước sauBước 1: Đặt
x
tan
t
,
suy ra
d
x
1
+
tan...
Đọc tiếp
Một học sinh làm bài tích phân I = ∫ 0 1 d x 1 + x 2 theo các bước sau
Bước 1: Đặt x = tan t , suy ra d x = 1 + tan 2 t d t
Bước 2: Đổi x = 1 ⇒ t = π 4 , x = 0 ⇒ t = 0
Bước 3: I = ∫ 0 π 4 1 + tan 2 t 1 + tan 2 t d t = ∫ 0 π 4 d t = t 0 π 4 = 0 − π 4 = − π 4
Các bước làm trên, bước nào bị sai
A. Bước 3
B. Bước 2
C. Không bước nào sai cả
D. Bước 1
cho pt x2 + 2(m - 2)x - m2 = 0 ( m là tham số)
a) Giải pt khi m = 0
b) Trong trường hợp pt có 2 nghiệm phân biệt x1, x2 (x1 < x2) . Tìm m sao cho |x1| - |x2| = 6
a) Khi m = 0 thì phương trình trở thành:
\(x^2+2\left(0-2\right)x-0^2=0\)
\(\Leftrightarrow x^2+2\cdot-2x-0=0\)
\(\Leftrightarrow x^2-4x=0\)
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
b) Ta có:
\(\left|x_1\right|-\left|x_2\right|=6\)
\(\Leftrightarrow x^2_1+x_2^2-2\left|x_1x_2\right|=36\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|=36\)
Mà: \(x_1+x_2=-2\left(m-2\right)=4-2m\)
\(x_1x_2=-m^2\)
\(\Leftrightarrow\left(4-2m\right)^2-2\cdot-m^2-2\cdot m^2=36\)
\(\Leftrightarrow16-16m+4m^2+2m^2-2m^2=36\)
\(\Leftrightarrow\left(4-2m\right)^2=6^2\)
\(\Leftrightarrow\left[{}\begin{matrix}4-2m=6\\4-2m=-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2m=-2\\2m=10\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giá trị của m làm cho phương trình
(
m
-
2
)
x
2
-
2
m
x
+
m
+
3
0
có hai nghiệm dương phân biệt là A. m 6 B. m 6 và m≠2 C. 2 m 6 hoặc m -3 D. m 0 hoặc 2 m 6
Đọc tiếp
Giá trị của m làm cho phương trình ( m - 2 ) x 2 - 2 m x + m + 3 = 0 có hai nghiệm dương phân biệt là
A. m > 6
B. m < 6 và m≠2
C. 2 < m < 6 hoặc m < -3
D. m < 0 hoặc 2 < m < 6
Chú ý:
Câu này có thể thử bằng máy tính bằng cách lần lượt thay các giá trị của m vào phương trình và tìm nghiệm của phương trình bậc hai tương ứng.
Thay m=7, phương trình vô nghiệm, loại A.
Thay m=-2, phương trình có một nghiệm âm, loại B, D.
Chọn C.
Đúng 0
Bình luận (0)
Cho phương trình x2 - 3x + m - 1 = 0 với m là tham số.
tim m để phương trình trên có 2 nghiệm phân biệt x1 , x2 sao cho 2x1 - 3x2 = 1
\(\text{Δ}=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
hay m<13/4
Áp dụng Vi-et, ta được: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-3x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=2\\x_2=1\end{matrix}\right.\)
Theo đề, ta có: m-1=2
hay m=3(nhận)
Đúng 2
Bình luận (0)
tìm m để phương trình: 3x^2 - 5x + m = 0 có 2 nghiệm phân biệt x1, x2 sao cho 6x1 + x2 = 0
Theo hệ thức Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\left(1\right)\\x_1x_2=\dfrac{m}{3}\left(2\right)\end{matrix}\right.\)
Ta có \(6x_1+x_2=0\)\(\Rightarrow5x_1+\left(x_1+x_2\right)=0\Rightarrow5x_1+\dfrac{5}{3}=0\Leftrightarrow x_1=-\dfrac{1}{3}\) Thay vào (1) ta được:
\(x_2-\dfrac{1}{3}=\dfrac{5}{3}\Rightarrow x_2=2\)
Thay \(x_1=-\dfrac{1}{3};x_2=2\) vào (2) ta được:
\(-\dfrac{2}{3}=\dfrac{m}{3}\Rightarrow m=-2\)
Đúng 2
Bình luận (0)
Bài 3: Cho phương trình: x2 – mx + 2m – 4 = 0 ( m là tham số) a) Giải phương trình với m = 1 b) Tìm m để phương trinh có hai nghiệm phân biệt x1; x2 sao cho x1 2 + x2 2 nhỏ nhất.
a: Thay m=1 vào pt, ta được:
\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
b: \(\text{Δ}=\left(-m\right)^2-4\left(2m-4\right)\)
\(=m^2-8m+16\)
\(=\left(m-4\right)^2\)
Để phươg trình có hai nghiệm phân biệt thì m-4<>0
hay m<>4
Theo đề, ta có: \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(-m\right)^2-2\left(2m-4\right)\)
\(=m^2-4m+8\)
\(=\left(m-2\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi m=2
Đúng 2
Bình luận (0)
Cho phương trình x2 - (m + 2)x + 3m - 6 = 0 (m là tham số)
Tìm các giá trị m để phương trình có hai nghiệm phân biệt x1,x2 sao cho \(\sqrt{x_1}\) +\(\sqrt{x_2}\) = 2
pt. 2 mghiemej pb
`<=>Delta>0`
`<=>(m+2)^2-4(3m-6)>0`
`<=>m^2+4m+4-12m+24>0`
`<=>m^2-8m+28>0`
`<=>(m-4)^2+8>0` luôn đúng
Áp dụng vi-ét ta có:`x_1+x_2=m+2,x_1.x_2=-3m-6`
`đk:x_1,x_2>=0=>x_1+x_2,x_1.x_2>=0`
`=>m+2>=0,3m-6>=0`
`<=>m>=2`
`pt<=>x_1+x_2+2sqrt(x_1.x_2)=4`
`<=>m+2+2sqrt{3m-6}=4`
`<=>3m+6+6sqrt(3m-6)=12`
`<=>3m-6+6sqrt(3m-6)=0`
`<=>3m-6=0`
`<=>m=2(tmđk)`
Vậy m=2
Đúng 1
Bình luận (0)
Cho hàm số y f(x) xác định và liên tục trên
0
;
+
∞
sao cho
x
2
+
x
.
f
e
x
+
f
e
x
1
với mọi
x
∈
0
;
+...
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên 0 ; + ∞ sao cho x 2 + x . f e x + f e x = 1 với mọi x ∈ 0 ; + ∞ Tính tích phân I = ∫ e e ln x . f ( x ) x d x .
A. I = - 1 8 .
B. I = - 2 3 .
C. I = 1 12 .
D. I = 3 8 .
Đáp án C
Phương pháp:
Đặt ẩn phụ t = ln x.
Cách giải:
Ta có:
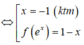
Đặt
Khi đó :
Đúng 0
Bình luận (0)