mn cho e hỏi cách chứng minh bđt cộng mẫu ạ
mn cho e hỏi cách giải chi tiết câu này với ạ:
Chứng minh rằng tam giác ABC vuông nếu sin^2A+sin^B+sin^2C=2
em cảm ơn ạ
\(sin^2A+sin^2B+sin^2C=2\)
\(\Leftrightarrow sin^2A+\dfrac{1-cos2B}{2}+\dfrac{1-cos2C}{2}=2\)
\(\Leftrightarrow sin^2A-\dfrac{1}{2}\left(cos2B+cos2C\right)=1\)
\(\Leftrightarrow1-cos^2A-cos\left(B+C\right)cos\left(B-C\right)=1\)
\(\Leftrightarrow cos^2A+cos\left(B+C\right)cos\left(B-C\right)=0\)
\(\Leftrightarrow cos^2A-cosA.cos\left(B-C\right)=0\)
\(\Leftrightarrow cosA\left[cosA-cos\left(B-C\right)\right]=0\)
\(\Leftrightarrow cosA.sin\left(\dfrac{A+B-C}{2}\right)sin\left(\dfrac{A+C-B}{2}\right)=0\)
\(\Leftrightarrow cosA.sin\left(90^0-C\right)sin\left(90^0-B\right)=0\)
\(\Leftrightarrow cosA.cosB.cosC=0\)
\(\Leftrightarrow\left[{}\begin{matrix}A=90^0\\B=90^0\\C=90^0\end{matrix}\right.\) hay tam giác ABC vuông
Cho mình hỏi lúc làm bài liên quan đến BĐT Cô si dạng Engel ấy ạ, lúc áp dụng BĐT này thì ở trên có cần phải chứng minh không ạ?
xài bđt phụ mới cần phải chứng minh nhé
mà tau nhớ làm gì có Cô si dạng Engel ??? ._.
Ý mày là không tồn tại cái BĐT tên Cosi dạng engel á:")?
Cauchy-Schwarz dạng Engel thì có :)) còn Cauchy dạng Engel chưa nghe bao giờ ???
các cao nhân cho em hỏi làm sao chứng minh BĐT Bunhiacopxki dạng phổ thông đc ạ
Phổ thông?Có phải dạng này không nhỉ?
`(ax+by)^2<=(a^2+b^2)(x^2+y^2)`
`<=>a^2x^2+b^2y^2+2axby<=a^2x^2+a^2y^2+b^2x^2+b^2y^2`
`<=>a^2y^2-2axby+b^2x^2>=0`
`<=>(ay-bx)^2>=0` luôn đúng
Dấu "=" `<=>ay=bx<=>a/x=b/y`
Mn ơi, cho e hỏi là tìm số trung bình cộng từ 1 đến 9 thì giải như nào ạ, e dg cần rất gấp, mong mn giúp đỡ ạ
Bạn sẽ tính (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) : 9 = 5
trung bình cộng từ 1 đến 9 là: `(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) : 9 = 5 `
Đáp số: `5`
Bạn tính (1+2+3+4+5+6+7+8+9) : 9 = 5 nhé.
Mn ơi cho em hỏi từ chỗ dấu bằng số 2 làm sao suy ra mẫu chung đó được vậy ạ? E cám ơn ạ
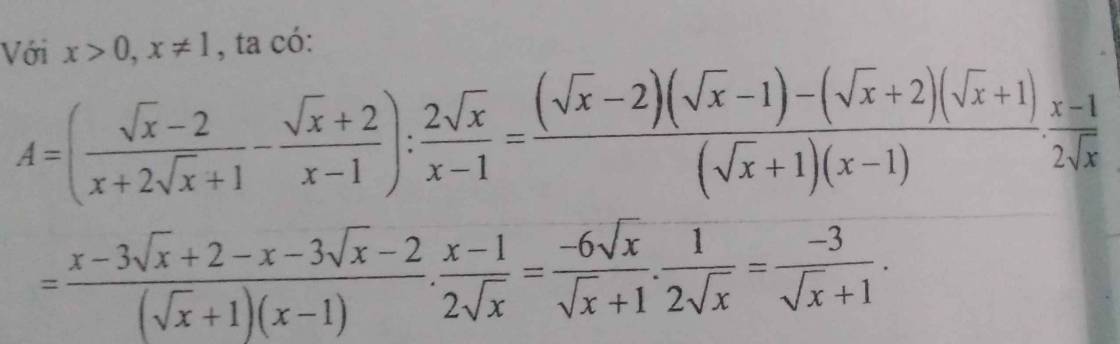
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}^2+2\sqrt{x}+1^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}^2-1^2}\right).\dfrac{x-1}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{x-1}{2\sqrt{x}}\)
Tới đây là có được mẫu chung ở dấu = thứ 2 rồi.
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\) ( với x>0;\(x\ne1\) )
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right].\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\dfrac{x-1}{2\sqrt{x}}\)
\(=.....\) ( theo như trên )
chứng minh bất đẳng thức:.1/a+1/b+1/c>=9/(a+b+c)
Ko áp dụng bđt cô-si có làm đc ko mn (ko giải cách lớp 9 nha). Ai có câu trả lời chính xác mình cho 3 tk.
nhân chéo lên
nhân a+b+c từ 9/a+b+c sang vế trái
vế phải còn 9
sau đó nhân vế trái ra
sử dụng bdt cosi là ra nha bn
1/a + 1/b + 1/c ≥ 9/(a+b+c)
<=> (1/a + 1/b + 1/c )(a+b+c) ≥ 9
Ta có : 1/a + 1/b + 1/c ≥ 3.căn bậc 3 1/abc
a+b+c ≥ 3 căn bậc 3 abc
(1/a + 1/b + 1/c)(a+c+c) ≥ 9 căn bậc 3 abc/abc = 9
<=> 1/a + 1/b + 1/c ≥ 9(a+b+c)
Dấu ''='' xảy ra khi : a=b =c
Mọi người ai có đề và cách giải của BĐT côsi ko ạ.. jup e với.. e cần 30 đề và cách giải ... c.on m.n nhiu
https://123doc.org/document/720452-cac-bai-toan-bat-dang-thuc-cosi-bai-tap-va-huong-dan-giai.htm
BẠN CÓ THỂ VÀO XEM
CHÚC BẠN HỌC TỐT
http://thuviengiaoan.vn/giao-an/chuyen-de-bat-dang-thuc-cosi-70748/
bạn có thể tham khảo thêm ở đây mình thấy khá hay và mình cũng đang học phần này, chúc bạn học tốt!
Cho tam giác MNP có MN = MP. Gọi E là trung điểm của MN
a. Chứng minh ME là tia phân giác của góc NMP
c. Chứng minh ME vuông góc NP
Vẽ hình nữa ạ, giúp em với ạ:(
Sai đề r, bạn kiểm tra lại đề nhé! R mik sẽ giúp bạn
a: Xét ΔMNP có MN=MP
nên ΔMNP cân tại M
mà ME là đường trung tuyến
nên ME là đường phân giác