\(ĐK:sinx-cosx\ne-2\)

\(< =>2y-1=sinx\left(1-y\right)+cosx\left(y+3\right)\)

Theo Bunhiacopxki:

\(\left[sinx\left(1-y\right)+cosx\left(y+3\right)\right]^2\)\(\le\left(sin^2x+cos^2x\right)\left[\left(1-y\right)^2+\left(y+3\right)^2\right]\)

\(< =>\left(2y-1\right)^2\le2y^2+4y+10\)

\(< =>2y^2-8y-9\le0\)

=> Bấm máy tìm Max, Min của y

(Sry máy tính của t bị ngáo không bấm ra)

\(\Rightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)

\(\Rightarrow\left(y-1\right)sinx-\left(y+3\right)cosx=1-2y\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất

\(\Rightarrow\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)

\(\Leftrightarrow2y^2-8y-9\le0\)

\(\Rightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)

\(y_{max}=\dfrac{4+\sqrt{34}}{2}\) ; \(y_{min}=\dfrac{4-\sqrt{34}}{2}\)

\(y=\dfrac{sinx+3cosx+1}{sinx-cosx+2}\)

\(\Leftrightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)

\(\Leftrightarrow\left(y-1\right)sinx-\left(y+3\right).cosx=1-2y\)

Phương trình có nghiệm khi \(\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)

\(\Leftrightarrow y^2-2y+1+y^2+6y+9\ge4y^2-4y+1\)

\(\Leftrightarrow2y^2-8y-9\le0\)

\(\Leftrightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)

Đáp án D

Đáp án B

Ta có y = 4 sin x − 3 cos x = 5 4 5 sinx − 3 5 cos x = 5 sin x − α  với   sin α = 3 5 cos α = 4 5

Ta có   − 1 ≤ sin x − α ≤ 1 ⇒ − 5 ≤ 5 sin x − α ≤ 5 ⇒ M = 5 m = − 5

\(-1\le cosx\le1\Rightarrow1\le y\le7\)

\(\Rightarrow y_{max}+y_{min}=7+1=8\)

 Ta có: \(-1\le cosx\le1\) \(\Rightarrow-3\le3cosx\le3\)

                                     \(\Rightarrow1\le3cosx+4\le7\)

Vậy \(y_{max}=7\); \(y_{min}=1\)

    \(\Rightarrow T=7+1=8\)

Chọn D

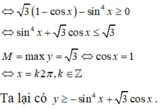
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có

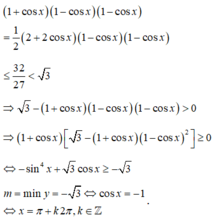
Do đó 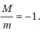. Vì vậy, mệnh đề D sai.

Ta có

sin 5 x ≤ sin 4 x ⇒ y ≤ sin 4 x + 3 cos x

Áp dụng bất đẳng thức Cauchy ta có:

1 - cos x 1 + cos x 1 + cos x = 1 2 2 - 2 cos x 1 + cos x 1 + cos x

≤ 1 2 2 - 2 cos x + ( 1 + cos x ) 2 3 3 = 32 27 < 3

⇒ 3 - 1 - cos x 1 + cos x 2 > 0 ⇒ 1 - cos x 3 - 1 - cos x 1 + cos x 2 ≥ 0 ⇒ 3 1 - cos x - sin 4 x ≥ 0 ⇔ sin 4 x + 3 cos x ≤ 3

M = maxy = 3 ⇔ cos(x) = 1

⇔ x = k 2 π ,   k ∈ ℤ

Ta lại có

y ≥ - sin 4 x + 3 cos x

Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có:

1 + cos x 1 - cos x 1 - cos x = 1 2 2 + 2 cos x 1 - cos x 2 ≥ 32 27 ≤ 3 ⇒ 3 - 1 + cos x 1 - cos x 2 > 0 ⇒ 1 + cos x 3 - 1 + cos x 1 - cos x 2 ⇔ sin 4 x + 3 cos x ≥ - 3 m = m i n y = - 3 ⇔ cos x = - 1 ⇔ x = k 2 π , k ∈ ℤ

Do đó M m = - 1 . Vì vậy, mệnh đề D sai.

Đáp án cần chọn là D

Câu 1:

$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$

Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$

Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.

Câu 2:

Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$

Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$

Với $x\in (1;3)$ thì hàm luôn nghịch biến

$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$

$\Rightarrow$ hàm không có min, max. 

Câu 3:

$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$

Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$

Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$

Đáp án D

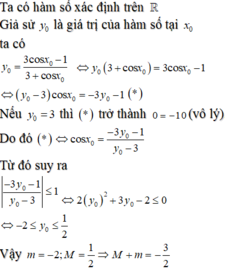
*Cách 2: Đặt ẩn phụ t = cos x đưa về hàm bậc nhất trên bậc nhất, rồi tìm min, max của hàm đó trên [-1;1]

Chọn đáp án D.