Tìm đạo hàm các hàm số sau:
y = x3 - 2x + 1
Những câu hỏi liên quan
Tìm khoảng đồng biến, nghịch biến của các hàm số sau:
y=x\(^4\)+4x2-3
y=x3+3x2+3x-2
a.
\(y'=4x^3+8x=4x\left(x^2+2\right)=0\Rightarrow x=0\)
Dấu của y':
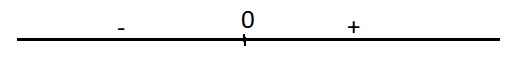
Hàm đồng biến trên \(\left(0;+\infty\right)\) và nghịch biến trên \(\left(-\infty;0\right)\)
b.
\(y'=3x^2+6x+3=3\left(x+1\right)^2\ge0\) ; \(\forall x\)
\(\Rightarrow\) Hàm đồng biến trên R
Đúng 0
Bình luận (0)
Bằng định nghĩa, tìm đạo hàm của hàm số sau: y = x 3 – 2 x + 1 tại x o = 2 .
Cách 1 : Áp dụng công thức
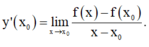
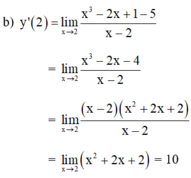
Cách 2 : Áp dụng công thức
Đúng 0
Bình luận (0)
27 tháng 4 2022 lúc 20:49
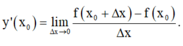
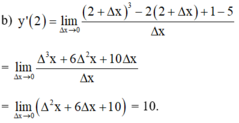
Tính đạo hàm của hàm số sau:
y=\(\dfrac{x^5}{5}+\sqrt{x}-\dfrac{1}{x}+\dfrac{1}{x^3}-2\)
\(y'=\dfrac{1}{5}\cdot5x^4+\dfrac{1}{2\sqrt{x}}+\dfrac{1}{x^2}+\dfrac{-\left(x^3\right)'}{x^6}\)
\(=x^4+\dfrac{1}{2\sqrt{x}}+\dfrac{1}{x^2}+\dfrac{-3x^2}{x^6}=x^4+\dfrac{1}{2\sqrt{x}}+\dfrac{1}{x^2}-\dfrac{3}{x^4}\)
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số
y
x
3
+
2
x
+
1
. A.
y
3
x
2
+
2
x
B.
y
3
x
2
+
2
C....
Đọc tiếp
Tính đạo hàm của hàm số y = x 3 + 2 x + 1 .
A. y ' = 3 x 2 + 2 x
B. y ' = 3 x 2 + 2
C. y ' = 3 x 2 + 2 x + 1
D. y ' = x 2 + 2
Tìm đạo hàm của các hàm số sau: y = x 1 - x 2 1 + x 3
8 tháng 11 2023 lúc 20:38
vẽ đồ thị hàm số sau:
y= -x2 - 2x - 1
Cho hàm số
f
(
x
)
(
m
-
1
)
x
3
+
2
x
-
m
+
1
Gọi S là tập chứa tất cả các giá trị thực của tham số m để hàm số có đạo hàm tại x 0. Số phần tử của tập S là A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho hàm số f ( x ) = ( m - 1 ) x 3 + 2 x - m + 1 Gọi S là tập chứa tất cả các giá trị thực của tham số m để hàm số có đạo hàm tại x = 0. Số phần tử của tập S là
A. 0
B. 1
C. 2
D. 3
28 tháng 2 2021 lúc 22:09
Cho hàm số y = f(x) có đạo hàm f'(x) = (x3 - 2x2)(x3 - 2x) với mọi x thuộc R. Hàm số \(\left|f\left(1-2018x\right)\right|\) có nhiều nhất bao nhiêu điểm cực trị?
\(g\left(x\right)=f\left(1-2018x\right)\Rightarrow g'\left(x\right)=-2018f'\left(1-2018x\right)\)
\(\Rightarrow\) Số nghiệm của \(g'\left(x\right)\) bằng số nghiệm \(f'\left(x\right)\Rightarrow g'\left(x\right)\) có 4 nghiệm
\(g\left(x\right)=0\Leftrightarrow f\left(1-2018x\right)=0\) có số nghiệm bằng số nghiệm f(x)
Do \(f'\left(x\right)\) có 4 nghiệm nên f(x) có tối đa 5 nghiệm
Vậy hàm có tối đa 9 cực trị
Đúng 1
Bình luận (0)
Tìm số f(x) x3 – 3x2 + 1. Đạo hàm của hàm số f(x) âm khi và chỉ khi. A. 0 x 2. B. x 1. C. x 0 hoặc x 1 D. x 0 hoặc x 2.
Đọc tiếp
Tìm số f(x) = x3 – 3x2 + 1. Đạo hàm của hàm số f(x) âm khi và chỉ khi.
A. 0 < x < 2.
B. x < 1.
C. x < 0 hoặc x > 1
D. x < 0 hoặc x > 2.
Chọn A.
Ta có: f’(x) = 3x2 – 6x.
f’(x) < 0 ⇔ 3x2 – 6x < 0 ⇔ 0 < x < 2.
Đúng 0
Bình luận (0)
Tìm nguyên hàm của các hàm số
f
(
x
)
x
3
-
2
x
+
5
thoả mãn F(1) 3 A.
F
(
x
)
x
4
4
-
x
2
+
5
x
-
5
4
B.
F
(
x...
Đọc tiếp
Tìm nguyên hàm của các hàm số f ( x ) = x 3 - 2 x + 5 thoả mãn F(1) = 3
A. F ( x ) = x 4 4 - x 2 + 5 x - 5 4
B. F ( x ) = x 4 4 - x 2 + 5 x - 3
C. F ( x ) = 4 x 4 - x 2 + 1 5 x - 5 4
D. F ( x ) = 4 x 4 - x 2 + 1 5 x + 3
