a: Xét tứ giác OBAC có 

\(\widehat{OBA}+\widehat{OCA}=180^0\)

Do đó: OBAC là tứ giác nội tiếp

Áp dụng BĐT Cô-si:

\(\dfrac{x^2}{x+1}+\dfrac{x+1}{9}\ge2\sqrt{\dfrac{x^2\left(x+1\right)}{9\left(x+1\right)}}=\dfrac{2}{3}x\)

\(\dfrac{y^2}{y+1}+\dfrac{y+1}{9}\ge2\sqrt{\dfrac{y^2\left(y+1\right)}{9\left(y+1\right)}}=\dfrac{2}{3}y\)

Cộng vế:

\(\dfrac{x^2}{x+1}+\dfrac{y^2}{y+1}+\dfrac{x+y+2}{9}\ge\dfrac{2}{3}\left(x+y\right)\)

\(\Leftrightarrow P+\dfrac{1+2}{9}\ge\dfrac{2}{3}.1\)

\(\Rightarrow P\ge\dfrac{1}{3}\)

\(P_{min}=\dfrac{1}{3}\) khi \(x=y=\dfrac{1}{2}\)

Áp dụng BĐT Cô-si:

\(3\left(a^2+4\right)\ge3.4a=12a\)

\(b^4+b^4+b^4+81\ge4\sqrt[4]{81b^{12}}=12b^3\)

Cộng vế:

\(3\left(a^2+b^4\right)+93\ge12\left(a+b^3\right)=384\)

\(\Rightarrow a^2+b^4\ge85\)

\(\Rightarrow P\ge85-19=66\)

\(P_{min}=66\) khi \(\left(a;b\right)=\left(2;3\right)\)

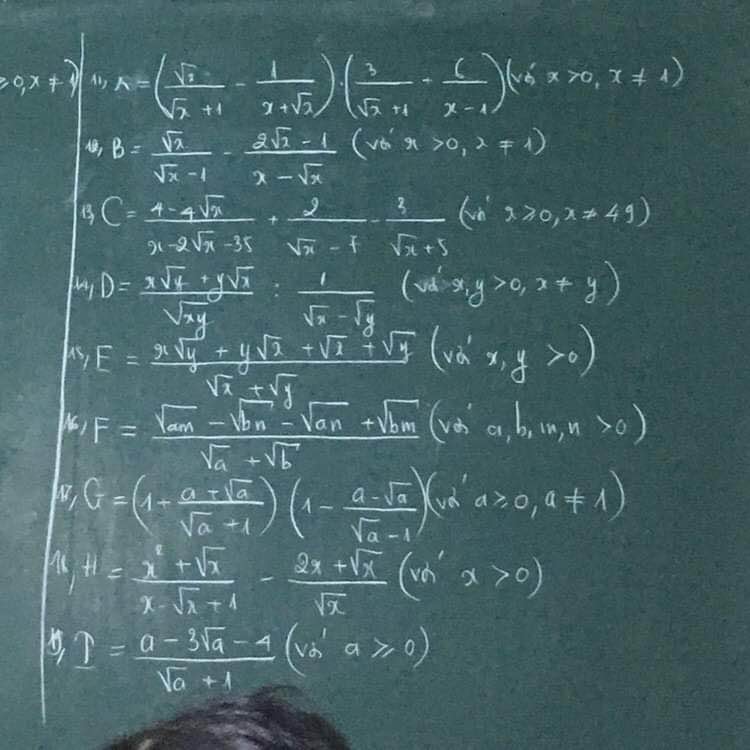
18) Ta có: \(H=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)

\(=\sqrt{x}\cdot\left(\sqrt{x}+1\right)-\left(2\sqrt{x}-1\right)\)

\(=x+\sqrt{x}-2\sqrt{x}+1\)

\(=x-\sqrt{x}+1\)

19) Ta có: \(T=\dfrac{a-3\sqrt{a}-4}{\sqrt{a}+1}\)

\(=\dfrac{\left(\sqrt{a}-4\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)

\(=\sqrt{a}-4\)

Chú bé loắt choắt

Cái xắc xinh xinh

Cái chân thoăn thoắt

Cái đầu nghênh nghênh

- Các cặp tiếng bắt vần với nhau là :

+ choắt - thoắt

+ xinh - nghênh

Từ "Vạn Xuân" : một vạn mùa xuân

Từ này đặt tên cho đất nước thể hiện lòng mong muốn cho sự trường tồn của dân tộc, của đất nước. Khẳng định ý chí giành độc lập của dân tộc, mong đất nước mãi mãi thanh bình, yên vui, tươi đẹp như một vạn mùa xuân.

))]

a

a

A

Đặt \(m=a^2,n=b^2\)

Ta đưa bài toán về dạng tìm GTLN và GTNN của \(A=m-3mn+2n\)

Khi đó ta suy ra từ giả thiết :

\(\left(m+n+1\right)^2+3mn+1=4m+5n\)

\(\Rightarrow m-3mn+2n=\left(m+n+1\right)^2+1-3m-3n\)

\(=\left(m^2+n^2+2mn+2m+2n+1\right)+1-3n-3m\)

\(=m^2+n^2+2mn-m-n+2\)

\(=m^2+m\left(2n-1\right)+n^2-n+2\)

\(=m^2+m\left(2n-1\right)+\frac{\left(2n-1\right)^2}{4}+\frac{7}{4}\)

\(=\left(m+\frac{2n-1}{2}\right)^2+\frac{7}{4}\ge\frac{7}{4}\)

Hay \(A\ge\frac{7}{4}\) . Đẳng thức xảy ra khi \(m=\frac{1-2n}{2}\)

Tới đây bạn tự suy ra nhé ^^