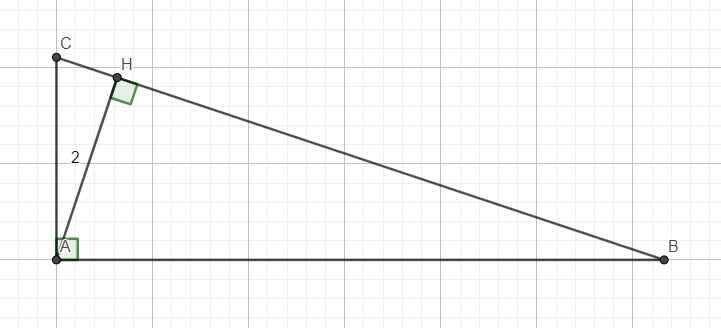
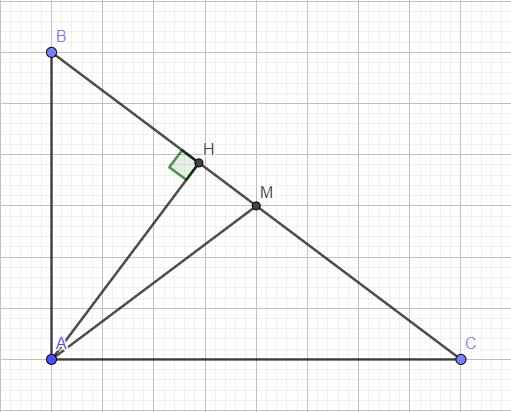
Cho tam giác ABC vuông tại A, AH uông góc với BC biết AB=4, AH=2. Tính HC. Mong mn giúp đỡ

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A , AH vuông góc với BC .Biết AB=7cm,AH=2cm.Tính HC. Mong mn giúp mình
Xét \(\Delta HAB\) vuông tại H \(\left(AH\perp BC\right)\),ta có:
\(AB^2=AH^2+BH^2\left(ĐLPytago\right)\\ \Rightarrow BH^2=AB^2-AH^2\\ \Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{7^2-2^2}=3\sqrt{5}\left(cm\right)\)
Xét \(\Delta ABC\) vuông tại A và có AH là đường cao \(\left(AH\perp BC\right)\),ta có:
\(AH^2=BH.CH\left(HTL\right)\\ \Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{2^2}{3\sqrt{5}}=\dfrac{4\sqrt{5}}{15}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC , kẻ AH vuông góc với BC , biết AB = 10cm,AH= 8cm, HC=15 cm. Tính chu vi tam giác tam giác ABC
Xem chi tiết
MONG MỌI NGƯỜI GIÚP ĐỠ .... YÊU MỌI NGƯỜI
Xét tam giác vuông ABH có:
\(AH^2+BH^2=AB^2\)(Đinh lý Pytagol)
\(\Rightarrow8^2+BH^2=10^2\)
\(\Rightarrow BH=6\)
Ta có:
BC=BH+HC=6+15=21
Xét tam giác vuông AHC có:
\(AH^2+HC^2=AC^2\)(Định lý Pytagol)
\(\Rightarrow8^2+15^2=AC^2\)
\(\Rightarrow AC=17\)
\(\Rightarrow\)Chu vi tam giác ABC là:
10+17+21=48(cm)
Vậy chu vi tam giác ABC là 48cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A, có AB=4, kẻ AH vuông góc với BC. Tính AH, mong mn giúp mình
ΔABC vuông cân tại A⇒AB=AC=4
Áp dụng hệ thức lượng ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{4^2}+\dfrac{1}{4^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{16}+\dfrac{1}{16}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{8}\\ \Rightarrow AH^2=8\\ \Rightarrow AH=\sqrt{8}\)
Đúng 0
Bình luận (0)
Vì ΔABC vuông cân tại A
⇒ AB = AC = 4 cm
Áp dụng dịnh lí Py-ta-go vào ΔABC vuông tại A ta có:
BC2=AB2+AC2=42+42=32
⇔BC=\(4\sqrt{2}\)
Ta có:AB.AC=AH.BC (hệ thức lượng)
⇔\(AH=\dfrac{AB.AC}{BC}=\dfrac{4.4}{4\sqrt{2}}=2\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A , kẻ AH vuông góc với BC, biết BH=4, CH=6. Tính AH .Mong mn giúp mình
Đúng 0
Bình luận (0)
Bài 1 cho tam giác ABC vuông tại A , AH vuông góc với BC tại H , AH =30 cm , HB:HC=5:6 . Tính AB BC AC
Bài 2 cho tam giác ABC vuông tại A , AH vuông góc với BC tại H . AB20 cm HC=9 cm Tính AH
MÌNH ĐANG CẦN GẤP TRONG TỐI NAY MONG CÁC BẠN GIÚP ĐỠ. XIN CHÂN THANH CAM ON VA HAU TA
hình tự vẽ nhé:
Áp dụng hệ thức lượng ta có:
\(AC^2=HC.BC=9BC\)
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(400+9BC=BC^2\)
\(\Leftrightarrow\)\(BC^2-9BC-400=0\)
\(\Leftrightarrow\)\(\left(BC-25\right)\left(BC+16\right)=0\)
\(\Leftrightarrow\)\(BC=25\)
\(\Rightarrow\)\(AC^2=9.25=225\)
\(\Rightarrow\)\(AC=\sqrt{225}=15\)
Áp dụng hệ thức lượng ta có:
\(AB.AC=AH.BC\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}\)
\(\Rightarrow\)\(AH=\frac{20.15}{25}=12\)
Đúng 0
Bình luận (0)
Mình đang cần gấp bài này. Mong các bạn giúp mình nhé. Cảm ơn các bạn
Bài 3: Cho tam giác ABC vuông tại A có AC=20cm. Kẻ AH vuông góc với BC. Biết BH=9cm,HC=16cm. Tính độ dài cạnh AB, AH?
Bài 6: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH=2cm,AB=4cm. Tính chu vi tam giác ABC.
Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AH vuông góc với BC,có AH=2, tan B=1/3. Tính AB, AC. Mong mn giúp mình
Trong tam giác vuông ABH ta có:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=6\)
Áp dụng định lý Pitago:
\(AB^2=AH^2+BH^2=40\)
\(\Rightarrow AB=2\sqrt{10}\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AC=AB.tanB=\dfrac{2\sqrt{10}}{3}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AH vuông góc với BC,M là trung điểm của BC, biết AB=3,AC=4.Tính độ dài HM, mong mn giúp mình
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=5\)
Trong tam giác vuông ABC, AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5}{2}\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông AHM:
\(HM=\sqrt{AM^2-AH^2}=\dfrac{7}{10}\)
Đúng 1
Bình luận (0)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}=\dfrac{25}{144}\)
\(\Leftrightarrow AH^2=\dfrac{144}{25}\)
hay AH=2,4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\dfrac{BC}{2}=\dfrac{5}{2}=2.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAMH vuông tại H, ta được:
\(AM^2=AH^2+HM^2\)
\(\Leftrightarrow HM^2=AM^2-AH^2=2.5^2-2.4^2=0.49\)
hay HM=0,7(cm)
Đúng 0
Bình luận (0)
1, Cho tam giác ABC ( góc A90 độ). Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với cạnh huyền BC tại D. C/m: BD^2-CD^2AB^22, Cho tam giác ABC( góc A90 độ). phân giác AD, đường cao AH. biết BD15cm, CD20cm, tính BH, CH3, Cho tam giác ABC( góc A90 độ). AB12cm, AC16cm, phân giác AD, đường cao AH. tính HB,HC,HD4, Cho tam giác ABC( góc A90 độ) đường cao AH. Tính chu vi tam giác ABC biết AH 14 cm, HB/HC1/4giúp đỡ mình nhé, mình đang cần gấp
Đọc tiếp
1, Cho tam giác ABC ( góc A=90 độ). Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với cạnh huyền BC tại D. C/m: BD^2-CD^2=AB^2
2, Cho tam giác ABC( góc A=90 độ). phân giác AD, đường cao AH. biết BD=15cm, CD=20cm, tính BH, CH
3, Cho tam giác ABC( góc A=90 độ). AB=12cm, AC=16cm, phân giác AD, đường cao AH. tính HB,HC,HD
4, Cho tam giác ABC( góc A=90 độ) đường cao AH. Tính chu vi tam giác ABC biết AH= 14 cm, HB/HC=1/4
giúp đỡ mình nhé, mình đang cần gấp
3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC có AH Vuông góc với BC , biết AH = 12 cm , BH = 9 cm , AC = 20 cm , AH vuông góc với BC
a/ tính độ dài các đoạn thẳng AB , HC
b/ tam giác ABC là tam giác gì ? vì sao
mong các bạn giúp mk nha mk cảm ơn
a/
∆ABC vuông tại A, AH, vuông góc BC
=> AB.AH = HB.AC
=> AB = 15Ta có: BC^2 = AB^2 + AC^2=> BC = 25=> HB = BC - BH = 25-9 = 16
Đúng 1
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm
Đúng 0
Bình luận (0)