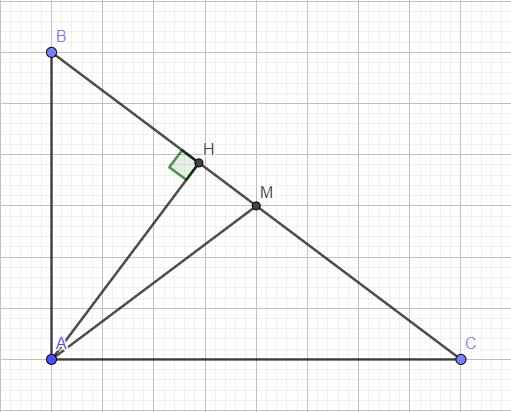
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=5\)
Trong tam giác vuông ABC, AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5}{2}\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông AHM:
\(HM=\sqrt{AM^2-AH^2}=\dfrac{7}{10}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}=\dfrac{25}{144}\)
\(\Leftrightarrow AH^2=\dfrac{144}{25}\)
hay AH=2,4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\dfrac{BC}{2}=\dfrac{5}{2}=2.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAMH vuông tại H, ta được:
\(AM^2=AH^2+HM^2\)
\(\Leftrightarrow HM^2=AM^2-AH^2=2.5^2-2.4^2=0.49\)
hay HM=0,7(cm)