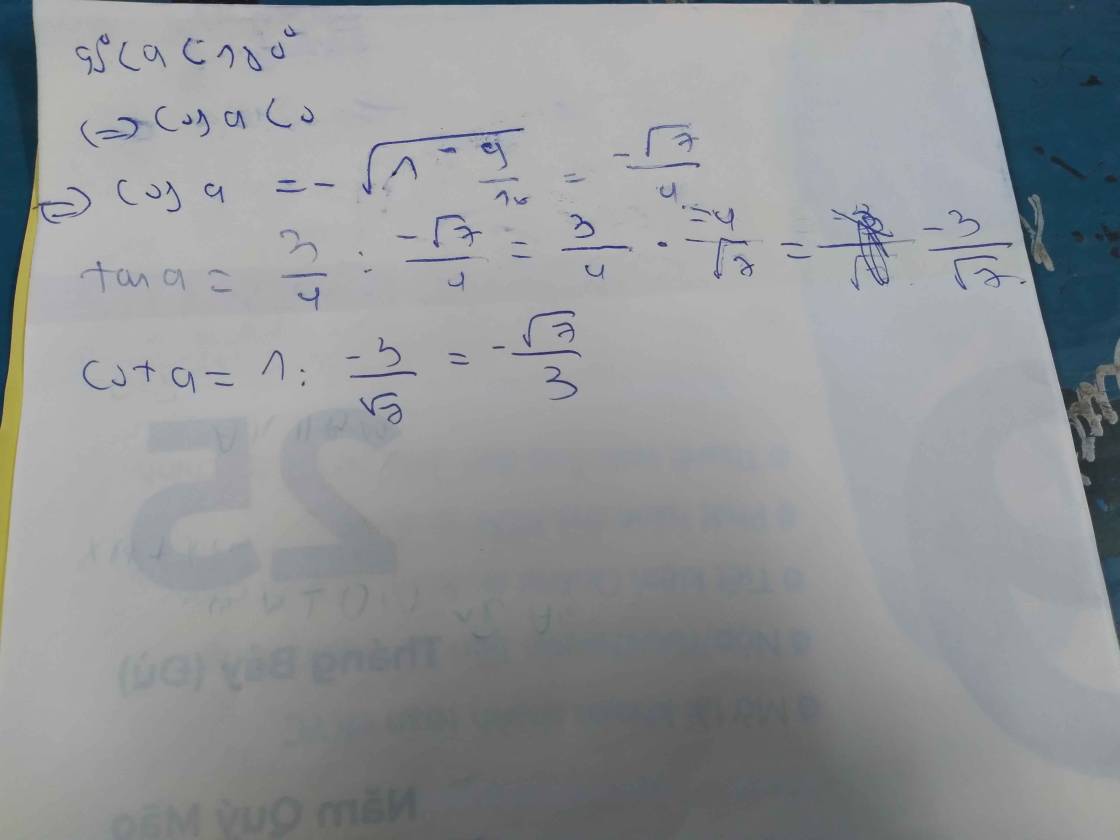4 cos mũ 2 alpha - 3 sin mũ 2 alpha biết cos anpha = 4/7

Những câu hỏi liên quan
cho tam giác ABC vuông tại A , đương cao AH biết AB =15 , AC =20
a, tính BC và BH
b, Cho alpha là một góc nhọn biết : sin alpha + cos alpha = 1,4
Tính : sin mũ 4 alpha -cos mũ 4 alpha
cho tam giác ABC vuông tại A , đương cao AH biết AB =15 , AC =20
a, tính BC và BH
b, Cho alpha là một góc nhọn biết : sin alpha + cos alpha = 1,4
Tính : sin mũ 4 alpha -cos mũ 4 alpha
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=25\)
Áp dụng HTL: \(BH=\dfrac{AB^2}{BC}=9\)
b, \(\sin\alpha+\cos\alpha=1,4\Leftrightarrow\left(\sin\alpha+\cos\alpha\right)^2=1,96\)
\(\Leftrightarrow\sin^2\alpha+\cos^2\alpha+2\sin\alpha\cdot\cos\alpha=1,96\\ \Leftrightarrow\sin\alpha\cdot\cos\alpha=\dfrac{1,96-1}{2}=\dfrac{0,96}{2}=0,48\)
\(\sin^4\alpha+\cos^4\alpha=\left(\sin^2\alpha+\cos^2\alpha\right)^2-2\sin^2\alpha\cdot\cos^2\alpha\\ =1^2+2\left(\sin\alpha\cdot\cos\alpha\right)^2=1+2\cdot\left(0,48\right)^2=1,4608\)
Đúng 1
Bình luận (0)
Cho sin alpha = 3/4. Alpha tù tính cos anpha tan alpha cot alpha
\(sin\alpha=\dfrac{3}{4}\)
\(sin^2\alpha+cos^2\alpha=1\)
\(\Leftrightarrow cos^2\alpha=1-sin^2\alpha\)
\(\Leftrightarrow cos^2\alpha=1-\dfrac{9}{16}=\dfrac{7}{16}\)
\(\Leftrightarrow cos\alpha=-\dfrac{\sqrt[]{7}}{4}\left(\dfrac{\pi}{2}< \alpha< \pi\right)\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\dfrac{3}{4}}{-\dfrac{\sqrt[]{7}}{4}}=-\dfrac{3}{\sqrt[]{7}}=-\dfrac{3\sqrt[]{7}}{7}\)
\(\Rightarrow cot\alpha=\dfrac{1}{tan\alpha}=-\dfrac{\sqrt[]{7}}{3}\)
Đúng 2
Bình luận (2)
Biết tan α=3. Tính giá trị các biểu thức sau:
a)\(\frac{\sin\alpha-\cos\alpha}{\sin\alpha+\cos\alpha}\)
b)\(\frac{2\sin\alpha+3\cos\alpha}{3\sin\alpha-5\cos\alpha}\)
c)\(\frac{1+2\cos^2\alpha}{\sin^2\alpha-\cos^2\alpha}\)
d)\(\frac{\sin^4\alpha+\cos^4\alpha}{1+\sin^2\alpha}\)
\(\frac{1}{cos^2a}=1+tan^2a\Rightarrow cos^2a=\frac{1}{1+tan^2a}=\frac{1}{10}\)
a/ \(\frac{sina-cosa}{sina+cosa}=\frac{\frac{sina}{cosa}-\frac{cosa}{cosa}}{\frac{sina}{cosa}+\frac{cosa}{cosa}}=\frac{tana-1}{tana+1}=\frac{3-1}{3+1}\)
b/ \(\frac{2sina+3cosa}{3sina-5cosa}=\frac{3tana+3}{3tana-5}=\frac{3.3+3}{3.3-5}\)
c/ \(\frac{1+2cos^2a}{1-cos^2a-cos^2a}=\frac{1+2cos^2a}{1-2cos^2a}=\frac{1+2.\frac{1}{10}}{1-2.\frac{1}{10}}\)
d/ \(\frac{\left(1-cos^2a\right)^2+\left(cos^2a\right)^2}{1+1-cos^2a}=\frac{\left(1-\frac{1}{10}\right)^2+\left(\frac{1}{10}\right)^2}{2-\frac{1}{10}}\)
Đúng 0
Bình luận (0)
Tính a) sin^4α - cos^4α , biết cos2α=3/5
b) cos(α-β) biết sinα - sinβ = 1/3 và cosα - cosβ = 1/2
tính :
\(E=\sin^6\alpha+\cos^6\alpha+3\sin^2\alpha\cdot\cos^2\alpha\)
\(F=3\sin^3\alpha+\cos^3\alpha-2\sin^6\alpha+\cos^6\alpha\)
\(G=\sqrt{\sin^4\alpha+4\cos^2\alpha}+\sqrt{\cos^4\alpha+4\sin^2\alpha}\)
E = sin^6 + cos^6 + 3sin^2.cos^2
= (sin^2 + cos^2)(sin^4 - sin^2.cos^2 + cos^4) + 3 sin^2.cos^2
= (sin^2 + cos^2)^2 - 3sin^2.cos^2 + 3sin^2.cos^2
= 1
Đúng 0
Bình luận (0)
1. Tìm x, biết: a. tan x+cot x2b. sin x.cos xfrac{sqrt{3}}{4}2. a. Biết tanalphafrac{1}{3}Tính Afrac{sinalpha-cosalpha}{sinalpha+cosalpha}b. Biết sinalphafrac{2}{3}Tính B3.sin^2alpha+4.cos^2alphac. Tính Csin^210^o+sin^220^o+sin^270^o+sin^280^od. Tính Dtan20^o.tan35^o.tan55^o.tan70^oe. Tính Esin^6alpha+cos^6alpha+3.sin^2alpha.cos^2alphaf. Tính F3.left(sin^3alpha+cos^3alpharight)-2.left(sin^6alpha+cos^6alpharight)g. Tính Gsqrt{sin^4alpha+4.cos^2alpha}+sqrt{cos^4alpha+4.sin^2alpha}Mọi người giúp mì...
Đọc tiếp
1. Tìm x, biết:
a. \(\tan x+\cot x=2\)
b. \(\sin x.\cos x=\frac{\sqrt{3}}{4}\)
2.
a. Biết \(\tan\alpha=\frac{1}{3}\)Tính A=\(\frac{\sin\alpha-\cos\alpha}{\sin\alpha+\cos\alpha}\)
b. Biết \(\sin\alpha=\frac{2}{3}\)Tính B=\(3.\sin^2\alpha+4.\cos^2\alpha\)
c. Tính C=\(\sin^210^o+\sin^220^o+\sin^270^o+\sin^280^o\)
d. Tính D=\(\tan20^o.\tan35^o.\tan55^o.\tan70^o\)
e. Tính E=\(\sin^6\alpha+\cos^6\alpha+3.\sin^2\alpha.\cos^2\alpha\)
f. Tính F=\(3.\left(\sin^3\alpha+\cos^3\alpha\right)-2.\left(\sin^6\alpha+\cos^6\alpha\right)\)
g. Tính G=\(\sqrt{\sin^4\alpha+4.\cos^2\alpha}+\sqrt{\cos^4\alpha+4.\sin^2\alpha}\)
Mọi người giúp mình với. Mình cảm ơn ạ!
Giúp mình vs chiều phải nộp bài rồi
a)C 4cos^2alpha-3sin^2alpha.cosfrac{4}{7}
b)cos^2alpha+cos^2beta+cos^2alpha.sin^2beta+sin^2alpha
c)2left(sinalpha-cosalpharight)^2-left(sinalpha+cosalpharight)^2+left(sinalpha.cosalpharight)
d)left(tanalpha-cotalpharight)^2-left(sinalpha+cotalpharight)^2
Đọc tiếp
Giúp mình vs chiều phải nộp bài rồi
a)C= \(4\cos^2\alpha-3\sin^2\alpha.cos=\frac{4}{7}\)
b)\(\cos^2\alpha+\cos^2\beta+\cos^2\alpha.\sin^2\beta+\sin^2\alpha\)
c)2\(\left(\sin\alpha-\cos\alpha\right)^2-\left(\sin\alpha+\cos\alpha\right)^2+\left(\sin\alpha.\cos\alpha\right)\)
d)\(\left(\tan\alpha-\cot\alpha\right)^2-\left(\sin\alpha+\cot\alpha\right)^2\)
Bạn không ghi rõ yêu cầu đề bài thì làm sao mà làm?
Đúng 0
Bình luận (1)
Cho góc nhọn alpha. Tính giá trị biểu thức:a) Aleft(sinalpha+cosalpharight)^2+left(sinalpha-cosalpharight)^2b) Bsin^4alphaleft(1+2cos^2alpharight)+cos^4alphaleft(1+2sin^2alpharight)c) Csin^6alpha+cos^6alpha+3sin^2alpha.cos^2alphad)
Dleft(3sinalpha+4cosalpharight)^2+left(4sinalpha-3cosalpharight)^2
Đọc tiếp
Cho góc nhọn \(\alpha\). Tính giá trị biểu thức:
a) \(A=\left(\sin\alpha+\cos\alpha\right)^2+\left(\sin\alpha-\cos\alpha\right)^2\)
b) \(B=\sin^4\alpha\left(1+2\cos^2\alpha\right)+\cos^4\alpha\left(1+2\sin^2\alpha\right)\)
c) \(C=\sin^6\alpha+\cos^6\alpha+3\sin^2\alpha.\cos^2\alpha\)
d)\( D=\left(3\sin\alpha+4\cos\alpha\right)^2+\left(4\sin\alpha-3\cos\alpha\right)^2\)