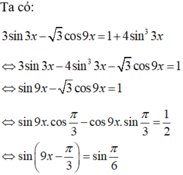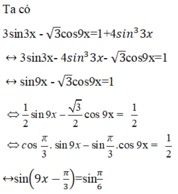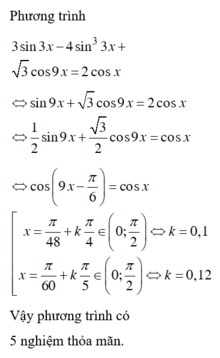Tại sao 3sin3x-4sin33x=sin9x

Những câu hỏi liên quan
Giải phương trình
3
sin
3
x
-
3
cos
9
x
1
+
4
sin
3
3
x
Đọc tiếp
Giải phương trình 3 sin 3 x - 3 cos 9 x = 1 + 4 sin 3 3 x
![]()
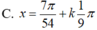
![]()
Tập nghiệm của phương trình
3
sin
3
x
-
3
cos
9
x
1
+
4
sin
3
3
x
là: A.
π
18
+
k
2
π
9
,
...
Đọc tiếp
Tập nghiệm của phương trình 3 sin 3 x - 3 cos 9 x = 1 + 4 sin 3 3 x là:
A. π 18 + k 2 π 9 , 7 π 54 + k 2 π 9 , k ∈ ℤ
B. π 18 ; 7 π 54
C. π 18 + k 2 π 9 , - π 54 + k 2 π 9 , k ∈ ℤ
D. ∅
Phương trình
3
sin
3
x
+
3
cos
9
x
2
cos
x
+
4
sin
3
3
x
có số nghiệm trên (0;
π
2
) là A. 2 B. 3 C. 4 D. lớn hơn hoặc bằng 5 nghiệm
Đọc tiếp
Phương trình 3 sin 3 x + 3 cos 9 x = 2 cos x + 4 sin 3 3 x có số nghiệm trên (0; π 2 ) là
A. 2
B. 3
C. 4
D. lớn hơn hoặc bằng 5 nghiệm
Phương trình
3
sin
3
x
+
3
cos
9
x
2
cos
x
+
4
sin
3
3
x
có số nghiệm trên
0
;
π
2
là: A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Phương trình 3 sin 3 x + 3 cos 9 x = 2 cos x + 4 sin 3 3 x có số nghiệm trên 0 ; π 2 là:
A. 2
B. 3
C. 4
D. 5
Phương trình sin9x=3sin3x có bao nhiêu nghiệm trong đoạn [0;180]
\(sin9x=3sin3x\Leftrightarrow3sin3x-4sin^33x=3sin3x\)
\(\Rightarrow sin^33x=0\Rightarrow sin3x=0\)
\(\Rightarrow3x=k\pi\Rightarrow x=\frac{k\pi}{3}\)
Do \(0\le x\le180\) (đề là \(180\) hay \(180\pi\) đây)
\(\Rightarrow0\le\frac{k\pi}{3}\le180\)
\(\Rightarrow0\le k\le\frac{540}{\pi}\)
\(\Rightarrow0\le k\le171\) (do \(k\in Z\))
Có \(172\) nghiệm
Đúng 0
Bình luận (0)
Phương trình : \(3sin3x+\sqrt{3}sin9x=1+4sin^33x\) có nghiệm là ?
\(3sin3x-4sin^33x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sin9x=1\)
\(\Leftrightarrow sin9x=\frac{1}{\sqrt{3}+1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+k2\pi\\x=\pi-\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+k2\pi\end{matrix}\right.\)
Bài 1: Tìm số nghiệm của phương trình \(cos^2-sin2x=\sqrt{2}+cos^2\left(\frac{\pi}{2}+x\right)\) trên khoảng (3;\(\pi\))
Bài 2: Giải phương trình: \(3sin3x+\sqrt{3}sin9x=1+4sin^33x\)
Bài 3: Giải phương trình: \(sin^2x+\sqrt{3}sinx.cosx=1\)
Câu 1:
\(cos^2\) gì nhỉ?
Câu 2: đề không hợp lý \(\sqrt{3}sin9x\) là \(\sqrt{3}cos9x\) có lý hơn
\(\Leftrightarrow3sin3x-4sin^33x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x=\frac{1}{\sqrt{3}+1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+\frac{k2\pi}{9}\\x=\frac{\pi}{9}-\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+\frac{k2\pi}{9}\end{matrix}\right.\)
Nghiệm nhìn rất ngớ ngẩn nếu đề đúng
3.
\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos2x+\frac{\sqrt{3}}{2}sin2x=1\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{6}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{6}=\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{6}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
cos2x/sin3x + cos6x/sin9x + cos18x/sin27x =0
ĐKXĐ: ....
\(\Leftrightarrow\frac{cos2x}{sin3x}+\frac{cos2\left(3x\right)}{sin3\left(3x\right)}+\frac{cos2\left(9x\right)}{sin3\left(9x\right)}=0\)
Xét biểu thức \(\frac{cos2a}{sin3a}=\frac{cos2a.sina}{sin3a.sina}=\frac{sin3a-sina}{2sin3a.sina}=\frac{1}{2}\left(\frac{1}{sina}-\frac{1}{sin3a}\right)\)
Vậy pt tương đương:
\(\frac{1}{2}\left(\frac{1}{sinx}-\frac{1}{sin3x}+\frac{1}{sin3x}-\frac{1}{sin9x}+\frac{1}{sin9x}-\frac{1}{sin27x}\right)=0\)
\(\Leftrightarrow\frac{1}{sinx}=\frac{1}{sin27x}\Leftrightarrow sinx=sin27x\Leftrightarrow...\)
Chứng minh: \(sin9x=sinx\left(1+2cos2x+2cos4x+2cos6x+2cos8x\right)\)