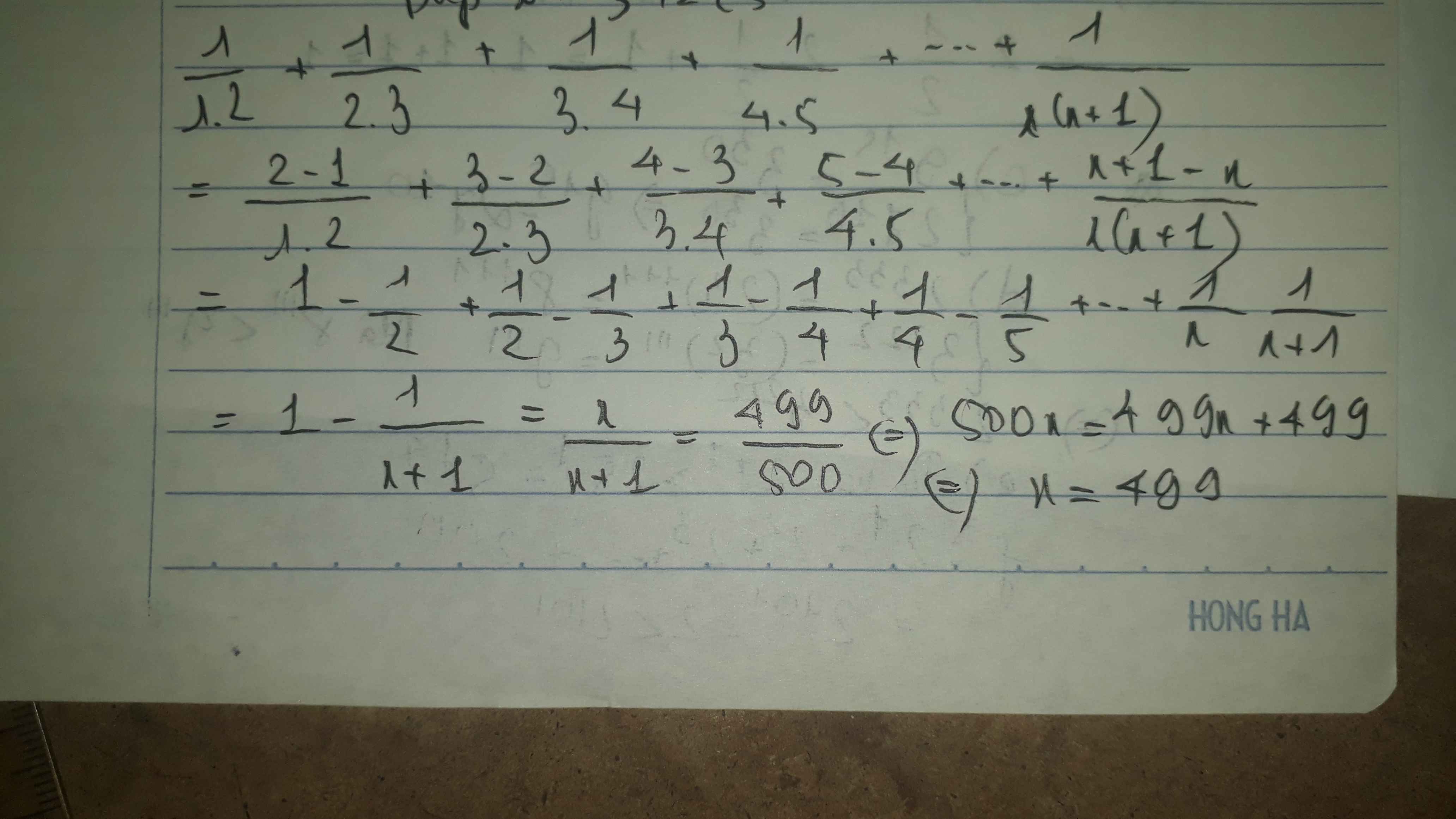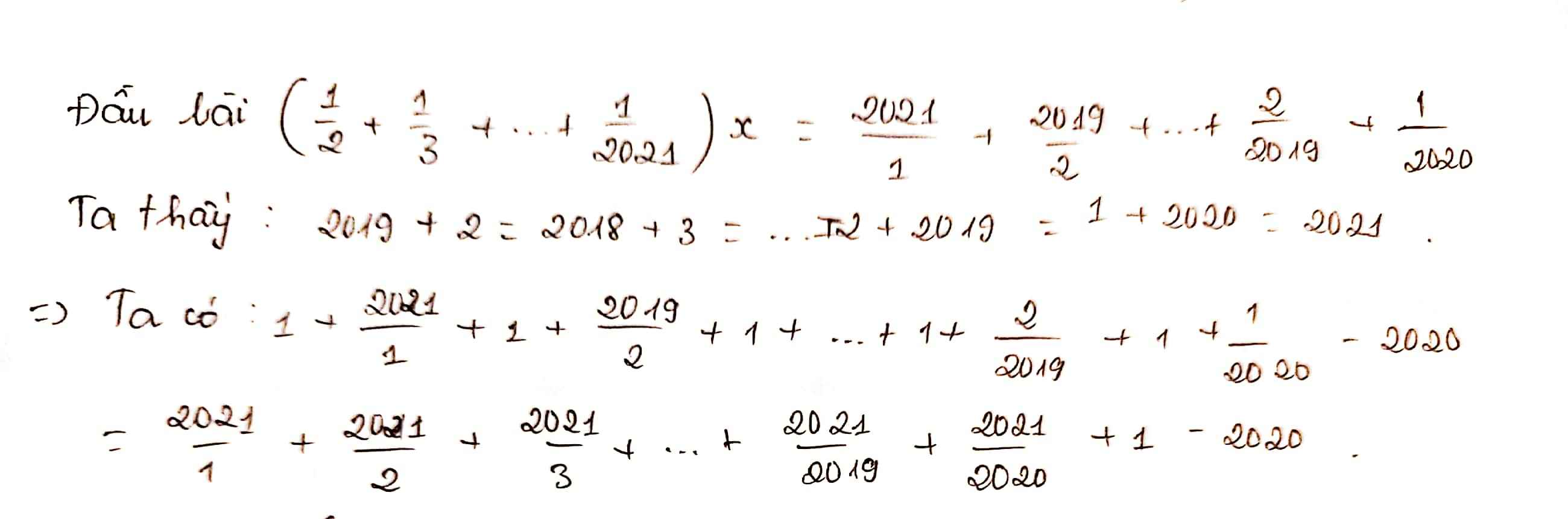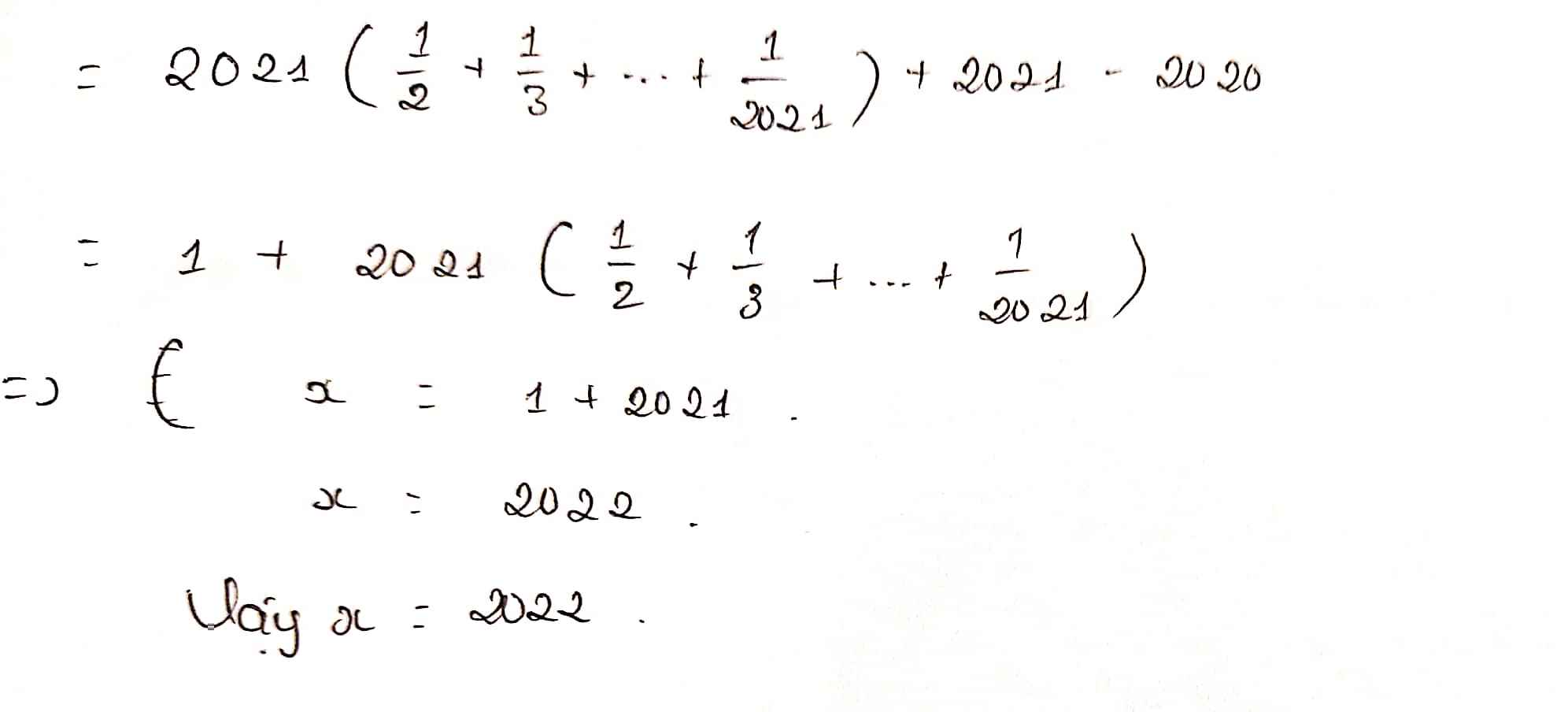(1+1/2).(1.1/3)x ...x(1+1/2019)

Những câu hỏi liên quan
tìm x biết :
1-(2x/3 +2)=-1.1/3
2/5x-1.1/2x+x=1/3
a) \(1-\left(\frac{2x}{3}+2\right)=-1\cdot\frac{1}{3}\)
\(1-\frac{2}{3}x-2=-\frac{1}{3}\)
\(-\frac{2}{3}x-1=-\frac{1}{3}\)
\(-\frac{2}{3}x=\frac{2}{3}\)
\(x=-1\)
----------------------------------------------------------
b) \(\frac{2}{5}x-1\cdot\frac{1}{2}x+x=\frac{1}{3}\)
\(\left(\frac{2}{5}-\frac{1}{2}+1\right)x=\frac{1}{3}\)
\(\frac{9}{10}x=\frac{1}{3}\)
\(x=\frac{1}{3}:\frac{9}{10}\)
\(x=\frac{10}{27}\)
Đúng 0
Bình luận (0)
1.1/2+1.2/3+1/3.4+1/4.5+..+1/x(x+1)=499/500
\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{x.\left(x+1\right)}=\dfrac{499}{500}\)
\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{499}{500}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{499}{500}\)
\(\Leftrightarrow x=499\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Nếu 1/3 + 1/6 +1/10 + ...... + 1/x.(x+1) : 2 = 2019/2021
A.x = 2019/2020 B. x = 2019 C. x = 2020 D. x = 2021
Xem thêm câu trả lời
A=[ 2020 x 2019 + 2019 x 2018] x [ 1 + 1/2 : 1 và 1/2 - 1 và 1/3]
\(A=\left(2020\times2019+2019\times2018\right)\times\left(1+\dfrac{1}{2}:1\dfrac{1}{2}-1\dfrac{1}{3}\right)\)
\(A=\left[2019\times\left(2020+2018\right)\right]\times\left(1+\dfrac{1}{2}:\dfrac{3}{2}-\dfrac{4}{3}\right)\)
\(A=4038\times2019\times\left(1+\dfrac{1}{3}-\dfrac{4}{3}\right)\)
\(A=4038\times2019\times0\)
\(A=0\)
Đúng 1
Bình luận (0)
x×2+x×1/5=1.1/3
\(x\times2+x\times\dfrac{1}{5}=1.\dfrac{1}{3}\\ \Rightarrow x\times\left(2+\dfrac{1}{5}\right)=\dfrac{1}{3}\\ \Rightarrow x\times\dfrac{11}{5}=\dfrac{1}{3}\\ \Rightarrow x=\dfrac{5}{33}\)
Đúng 0
Bình luận (0)
Tìm x biết:
( 1/2 + 1/3 + ... + 1/2021 ).x = 2021/1 +2019/2 + ... + 2/2019 + 1/2020
Tìm x biết:
( 1/2 + 1/3 + ... + 1/2021 ).x = 2021/1 +2019/2 + ... + 2/2019 + 1/2020
Cho A = 1/3 + 1/3^2 + 1/3^3 + .....+ 1/3^2018 + 1/3^2019 . Tìm x để : [ 2A + 1/3^2019 ] . x = 2
Ta có A = \(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{2019}}\)(1)
=> 3A = \(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2018}}\)(2)
Lấy (2) trừ (1) theo vế ta có :
3A - A = \(\left(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2018}}\right)-\left(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{2019}}\right)\)
2A = \(1-\frac{1}{3^{2019}}\)
Khi đó : \(\left(2A+\frac{1}{3^{2019}}\right).x=2\)
\(\Leftrightarrow\left(1-\frac{1}{3^{2019}}+\frac{1}{3^{2019}}\right).x=2\)
\(\Rightarrow x=2\)
1.1/3-2√2 + 1/2+√5 2.1/√3+√7 + 2/1-√7 3.a-2√a/2-√a 4.x√y+y√x/√x+√y
1: \(\dfrac{1}{3-2\sqrt{2}}+\dfrac{1}{\sqrt{5}+2}\)
\(=\dfrac{3+2\sqrt{2}}{1}+\dfrac{\sqrt{5}-2}{1}\)
\(=3+2\sqrt{2}+\sqrt{5}-2=2\sqrt{2}+\sqrt{5}+1\)
2: \(\dfrac{1}{\sqrt{3}+\sqrt{7}}+\dfrac{2}{1-\sqrt{7}}\)
\(=\dfrac{\sqrt{7}-\sqrt{3}}{4}+\dfrac{2\left(1+\sqrt{7}\right)}{-6}\)
\(=\dfrac{\sqrt{7}-\sqrt{3}}{4}-\dfrac{1+\sqrt{7}}{3}\)
\(=\dfrac{3\left(\sqrt{7}-\sqrt{3}\right)-4\left(\sqrt{7}+1\right)}{12}=\dfrac{-\sqrt{7}-3\sqrt{3}-4}{12}\)
3:
\(=\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{2-\sqrt{a}}=-\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{\sqrt{a}-2}=-\sqrt{a}\)
4:
\(=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\)
\(=\sqrt{xy}\)
Đúng 1
Bình luận (0)
1) \(\dfrac{1}{3-2\sqrt{2}}+\dfrac{1}{\sqrt{5}+2}\)
\(=\dfrac{3+2\sqrt{2}}{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}+\dfrac{\sqrt{5}-2}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}\)
\(=\dfrac{3+2\sqrt{2}}{3^2-\left(2\sqrt{2}\right)^2}+\dfrac{\sqrt{5}-2}{\left(\sqrt{5}\right)^2-2^2}\)
\(=\dfrac{3+2\sqrt{2}}{1}+\dfrac{\sqrt{5}-2}{1}\)
\(=3+2\sqrt{2}+\sqrt{5}-2\)
\(=2\sqrt{2}+\sqrt{5}+1\)
2) \(\dfrac{1}{\sqrt{3}-\sqrt{7}}+\dfrac{2}{1-\sqrt{7}}\)
\(=\dfrac{\sqrt{3}+\sqrt{7}}{\left(\sqrt{3}+\sqrt{7}\right)\left(\sqrt{3}-\sqrt{7}\right)}+\dfrac{2\cdot\left(1+\sqrt{7}\right)}{\left(1-\sqrt{7}\right)\left(1+\sqrt{7}\right)}\)
\(=\dfrac{\sqrt{3}+\sqrt{7}}{\left(\sqrt{3}\right)^2-\left(\sqrt{7}\right)^2}+\dfrac{2\cdot\left(1+\sqrt{7}\right)}{1^2-\left(\sqrt{7}\right)^2}\)
\(=\dfrac{-\sqrt{3}-\sqrt{7}}{4}-\dfrac{2\cdot\left(1+\sqrt{7}\right)}{6}\)
\(=\dfrac{-\sqrt{3}-\sqrt{7}}{4}-\dfrac{1+\sqrt{7}}{3}\)
\(=\dfrac{-3\sqrt{3}-3\sqrt{7}}{12}-\dfrac{4+4\sqrt{7}}{12}\)
\(=\dfrac{-3\sqrt{3}-3\sqrt{7}-4-4\sqrt{7}}{12}\)
\(=\dfrac{-3\sqrt{3}-7\sqrt{7}-4}{12}\)
3) \(\dfrac{a-2\sqrt{a}}{2-\sqrt{a}}\)
\(=-\dfrac{a-2\sqrt{a}}{\sqrt{a}-2}\)
\(=-\dfrac{\sqrt{a}\cdot\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\)
\(=-\sqrt{a}\)
4) \(\dfrac{x\sqrt{y}+y\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{\sqrt{x}\cdot\sqrt{xy}+\sqrt{y}\cdot\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{\sqrt{xy}\cdot\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\)
\(=\sqrt{xy}\)
Đúng 0
Bình luận (1)