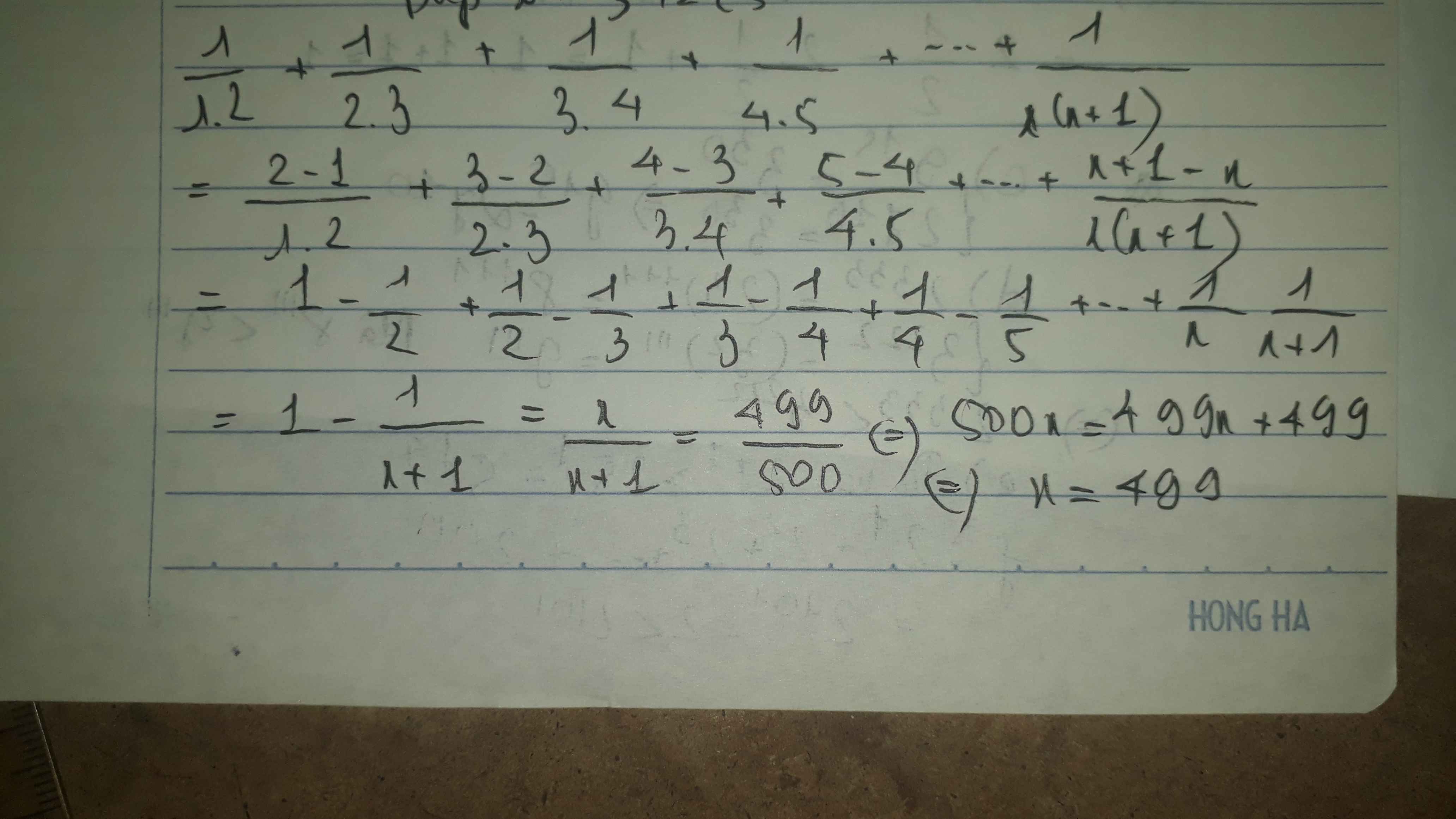\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{x.\left(x+1\right)}=\dfrac{499}{500}\)
\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{499}{500}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{499}{500}\)
\(\Leftrightarrow x=499\)
Ta có: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{499}{500}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{499}{500}\)
\(\Leftrightarrow x=499\)