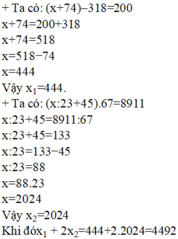Dùng phương pháp chặn :

x \(\le\) y \(\le\) z \(\Rightarrow\) x² \(\le\) y² \(\le\) z² \(\Rightarrow\) x² + y² + z² \(\le\) 3z² 

\(\Rightarrow\) 3z² \(\ge\) 34 \(\Leftrightarrow\) z² \(\ge\) 34/3  (1)

x² + y² + z²  = 34 mà x,y,z \(\in\) N \(\Rightarrow\) z² \(\le\) 34 (2)

Kết hợp (1) và (2) ta có : 

34/3  \(\le\) z² \(\le\)  34 

\(\Rightarrow\) z² \(\in\) { 16; 25}

vì z \(\in\) N\(\Rightarrow\) z \(\in\) { 4; 5}

th1 Z = 4 ta có :

x² + y² + 16 = 34

x² + y² = 12 

x \(\le\) y \(\Rightarrow\) x² \(\le\)y² \(\Rightarrow\) x² + y² \(\le\) 2y² \(\Rightarrow\) 12 \(\le\)2y² \(\Rightarrow\) y² \(\ge\) 6 (*)

x² + y² = 12 \(\Rightarrow\) y² \(\le\) 12 (**)

Kết hợp (*) và (**) ta có :

6 \(\le\) y² \(\le\) 12 \(\Rightarrow\) y² = 9 vì y \(\in\) N\(\Rightarrow\) y = 3

với y = 3 ta có : x² + 3² = 12 \(\Rightarrow\) x² = 12-9 = 3 \(\Rightarrow\) x = +- \(\sqrt{3}\)(loại vì x \(\in\) N)

th2 : z = 5 ta có :

x² + y² + 25 = 34

\(\Rightarrow\) x² + y² = 34 - 25  = 9

x \(\le\) y \(\Rightarrow\) x² \(\le\) y² \(\Rightarrow\) x² + y² \(\le\)2y² \(\Rightarrow\) 2y² \(\ge\) 9 \(\Rightarrow\) y² \(\ge\) 9/2 (a)

x² + y² = 9 \(\Rightarrow\) y² \(\le\) 9 (b)

Kết hợp (a) và (b) ta có :

9/2 \(\le\) y² \(\le\) 9 \(\Rightarrow\) y² = 9 vì y \(\in\) N \(\Rightarrow\) y = 3

với y = 3 \(\Rightarrow\) x² + 3² = 9 \(\Rightarrow\) x² = 0 \(\Rightarrow\) x = 0

kết luận (x; y; z) =( 0; 3; 5) là nghiệm duy nhất thỏa mãn pt 

Đáp án cần chọn là: B

1.

\(5=3xy+x+y\ge3xy+2\sqrt{xy}\)

\(\Leftrightarrow\left(\sqrt{xy}-1\right)\left(3\sqrt{xy}+5\right)\le0\Rightarrow xy\le1\)

\(P=\dfrac{\left(x+1\right)\left(x^2+1\right)+\left(y+1\right)\left(y^2+1\right)}{\left(x^2+1\right)\left(y^2+1\right)}-\sqrt{9-5xy}\)

\(P=\dfrac{\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy+x+y+2}{x^2y^2+\left(x+y\right)^2-2xy+1}-\sqrt{9-5xy}\)

Đặt \(xy=a\Rightarrow0< a\le1\)

\(P=\dfrac{\left(5-3a\right)^3-3a\left(5-3a\right)+\left(5-3a\right)^2-2a+5-3a+2}{a^2+\left(5-3a\right)^2-2a+1}-\sqrt{9-5a}\)

\(P=\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{2}.2\sqrt{9-5a}\)

\(P\ge\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{4}\left(4+9-5a\right)\)

\(P\ge\dfrac{-29a^3+161a^2-277a+145}{4\left(5a^2-16a+13\right)}=\dfrac{\left(1-a\right)\left(29a^2-132a+145\right)}{4\left(5a^2-16a+13\right)}\)

\(P\ge\dfrac{\left(1-a\right)\left[29a^2+132\left(1-a\right)+13\right]}{4\left(5a^2-16a+13\right)}\ge0\)

\(P_{min}=0\) khi \(a=1\) hay \(x=y=1\)

Hai phân thức của P rất khó làm gọn bằng AM-GM hoặc Cauchy-Schwarz (nó hơi chặt)

2.

Đặt \(A=9^n+62\)

Do \(9^n⋮3\) với mọi \(n\in Z^+\) và 62 ko chia hết cho 3 nên \(A⋮̸3\)

Mặt khác tích của k số lẻ liên tiếp sẽ luôn chia hết cho 3 nếu \(k\ge3\)

\(\Rightarrow\) Bài toán thỏa mãn khi và chỉ khi \(k=2\)

Do tích của 2 số lẻ liên tiếp đều không chia hết cho 3, gọi 2 số đó lần lượt là \(6m-1\)  và \(6m+1\)

\(\Leftrightarrow\left(6m-1\right)\left(6m+1\right)=9^n+62\)

\(\Leftrightarrow36m^2=9^n+63\)

\(\Leftrightarrow4m^2=9^{n-1}+7\)

\(\Leftrightarrow\left(2m\right)^2-\left(3^{n-1}\right)^2=7\)

\(\Leftrightarrow\left(2m-3^{n-1}\right)\left(2m+3^{n-1}\right)=7\)

Pt ước số cơ bản, bạn tự giải tiếp

Bài 2:

Gọi số ban đầu là \(\overline{ab}\)

Theo đề, ta có: 5a+2b=29 và 10b+a-10a-b=36

=>5a+2b=29 và -9a+9b=36

=>a=3 và b=7

Ta có:(x,y) = 1 =>x, y nguyên tố cùng nhau

(LOẠI) (NHÂN)

Vậy x = 3;y = 4

Ta có:(x,y) = 1 =>x, y nguyên tố cùng nhau

(LOẠI) (NHÂN)

Vậy x = 3;y = 4

a) Áp dụng bất đẳng thức Cosi ta có :

\(x^2+1\geq 2x\\ 4y^2+1\geq 4y\\ 9z^2+1\geq 6z\)

Suy ra \(S\leq 6\)

Dấu = xảy ra khi \(x=1;y=\frac{1}{2}; z=\frac{1}{3}\)

Với: y=0 thì: \(-x^2+13x=-24\text{ nên: }x^2-13x-24=0\text{ thấy ngay phương trình này ko có nghiệm nguyên}\)

\(\text{Nếu: }y>0\text{ thì: }x^2-13x=23+11^y\text{ do đó: }\left(x-1\right)^2-11x=24+11^y\text{ do đó: }\left(x-1\right)^2\text{ chia 11 dư 2}\)

THấy ngay 1 số chia 11 dư 0;+-1 ; +-2; +-3;....;+-5 mà: 0;1;4;9;16;25 không có số nào chia 11 dư 2 nên loại nên phương trình vô nghiệm

Lời giải:

PT $\Leftrightarrow 11^y=x^2-13x-23$

Nếu $x\equiv 0\pmod 3$ thì:

$x^2-13x-23\equiv -23\equiv 1\pmod 3$

Nếu $x\equiv 1\pmod 3$ thì:

$x^2-13x-23\equiv 1-13-23\equiv 1\pmod 3$

Nếu $x\equiv 2\pmod 3$ thì:

$x^2-13x-23\equiv 1-13.2-23\equiv 0\pmod 3$

Do đó $11^y\equiv 0\pmod 3$ (vô lý) hoặc $11^y\equiv 1\pmod 3$

$\Rightarrow (-1)^y\equiv 1\pmod 3$

$\Rightarrow y$ chẵn. Đặt $y=2t$

$11^{2t}-x^2+13x+23=0$

$(2.11^{t})^2-(2x-13)^2=-261$

$(2.11^t-2x-13)(2.11^t+2x+13)=-261$

Đến đây là dạng phương trình tích cơ bản. Bạn có thể dễ dàng giải.

Lời giải:

PT $\Leftrightarrow 11^y=x^2-13x-23$

Nếu $x\equiv 0\pmod 3$ thì:

$x^2-13x-23\equiv -23\equiv 1\pmod 3$

Nếu $x\equiv 1\pmod 3$ thì:

$x^2-13x-23\equiv 1-13-23\equiv 1\pmod 3$

Nếu $x\equiv 2\pmod 3$ thì:

$x^2-13x-23\equiv 1-13.2-23\equiv 0\pmod 3$

Do đó $11^y\equiv 0\pmod 3$ (vô lý) hoặc $11^y\equiv 1\pmod 3$

$\Rightarrow (-1)^y\equiv 1\pmod 3$

$\Rightarrow y$ chẵn. Đặt $y=2t$

$11^{2t}-x^2+13x+23=0$

$(2.11^{t})^2-(2x-13)^2=-261$

$(2.11^t-2x-13)(2.11^t+2x+13)=-261$

Đến đây là dạng phương trình tích cơ bản. Bạn có thể dễ dàng giải.