Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
a) -\(\frac{1}{3}\)x2y và 2xy3;
b) \(\frac{1}{4}\)x3y và -2x3y5
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được: - 1 3 x 2 y v à 2 x y 3
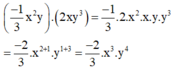
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 3 ; số mũ của biến y là 4
⇒ Bậc của đơn thức đó là 3+4=7.
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
a) -1/3x2y và 2xy3;
b) 1/4x3y và -2x3y5.
a,(-1/3)x2y.2xy3
=(-1/3).3.2.2.xy
=-1.4.xy
=-4xy
b,1/4xy3.(-2)x3y5
=1/4.(-2).5.3.3.xy
=1/4.-10.9xy
=-5/2.9xy
=-45/2xy
làm mk bài này với
2y(-x)^3 và -1/2xy^4
Tính tích các đơn thức sau và tìm bậc của đơn thức thu được.
a) 4xy2 và -3/4 ( x2y)3 ;
b) 1/6x(2y3)2 và -9x5y.
Bài 4: Tính tích các đơn thức sau rồi tìm bậc của đơn thức nhận được:
a) 2 5
x
18
y và 3 2 18x y .
b) 2 2
x
9
y và 36x2 y3
Bài 2: Tính tích các đơn thức sau và tìm bậc của đơn thức thu được:
a, và
b,
;
và
c, ;
và
Bài 3: Tính giá trị của các đơn thức sau:
a, tại x = -1,
b, tại x = -2, y = 1
c, tại x = -6, y = -1, a là hằng số
\(2,\\ a,=-3x^3y^3z^4\\ b,=\dfrac{1}{4}xy^2\cdot\dfrac{1}{4}x^4y^4\cdot\left(-\dfrac{4}{5}yz^2\right)=-\dfrac{1}{20}x^5y^7z^2\\ c,=-\dfrac{15}{14}x^6y^{11}z^{10}\\ 3,\\ a,=9\left(-1\right)\left(-\dfrac{1}{27}\right)=\dfrac{1}{3}\\ b,=-\dfrac{1}{5}\left(-8\right)=\dfrac{8}{5}\\ c,=\dfrac{4}{9}a\cdot36\left(-1\right)=-16a\)
Viết các đa thức sau dưới dạng tổng của các đơn thức rồi thu gọn các đơn thức đồng dạng(nếu có)và tìm bậc của những đa thức đó với tập hợp các biến.
a) (x2 - y2) (x2 + y2) - 3xy2(x + y) + 5x2y2 + x2y(x - y)
b) 3x(x2y + xy2) - 7xy(x2 - y2) - x(3y2 - 2xy2 - 5y - 1)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
1 4 x 3 y v à - 2 x 3 y 5

Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 6 ; số mũ của biến y là 6.
⇒ Bậc của đơn thức đó là 6+6 = 12
cho đơn thức: A=(-1/2 x2y).(2/3 xy2)
a) thu gọn và tìm bậc của đơn thức A
b)tính giá trị của đơn thức A khi x=-1 và y=2
a)\(A=\left(-\dfrac{1}{2}\cdot\dfrac{2}{3}\right)\left(x^2x\right)\left(yy^2\right)\)
\(A=-\dfrac{1}{3}x^3y^3\)
bậc : 3+3=6
b)thay x=-1 và y=2 vào A ta đc
\(A=-\dfrac{1}{3}.\left(-1\right)^3.2^3=-\dfrac{1}{3}.\left(-1\right).8=\dfrac{8}{3}\)
tính tích của các đơn thức sau rồi tìm Bậc của đơn thức thu được:\(\left(\dfrac{-1}{3}x^2y\right)\times\left(6xy^2\right)\)
`(-1/3 x^2 y) .(6xy^2)`
`=(-1/3 . 6).(x^2.x).(y.y^2)`
`=-2 x^3 y^3`
Bậc của đơn thức là `6`
Bài 2: Tính tích của các đơn thức sau, rồi tìm bậc của đơn thức thu được:
a) 2x2y và – 11xy4 ; b) x3y2 và xy5z7
\(a.\left(2x^2y\right).\left(-11xy^4\right)=-22x^3y^5\)
bậc là: 8
\(b.\left(x^3y^2\right).\left(xy^5z^7\right)=x^4y^7z^7\)
bậc là: 18
`a) ( 2x^2 y ) . ( -11xy^4)`
`= [ 2 . (-11) ] ( x^2 . x ) ( y . y^4 )`
`= -22x^3y^5`
`->` Bậc : `3 + 5 = 8`
`b) ( x^3y^2 ) . ( xy^5z^7 )`
`= ( x^3 . x ) ( y^2 . y^5 ) z^7`
`= x^4y^7z^7`
`->` Bậc: `4 + 7 + 7 = 18`