Qua một điểm M ở ngoài (O;R) ta kẻ cát tuyến MAB qua tâm O và cát tuyến MCD. Kẻ tiếp tuyến MT. Chứng minh rằng:
a. MA.MB = MC.MD = MT2
b. △MTC đồng dạng ▲ MDT
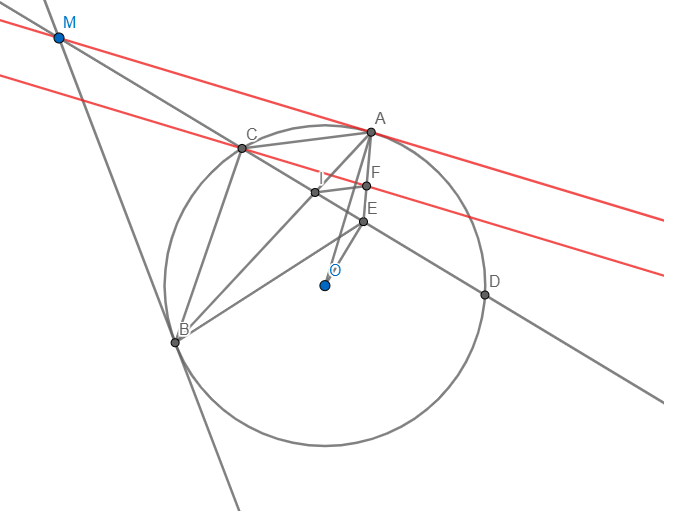
MỌI NGƯỜI ƠI GIÚP MÌNH ĐI ![]() ✰ Cho đường tròn O,R và một đường thẳng d cắt O tại tại CD . một điểm M di chuyển trên d sao cho MC > MD và ở ngoài O qua M kẻ 2 tiếp tuyến MA , MB . Gọi H là trung điểm của CD và giao điểm của AB với MO , với OH lần lượt là E, F . Đoạn thẳng OM cắt cung nhỏ tại I
✰ Cho đường tròn O,R và một đường thẳng d cắt O tại tại CD . một điểm M di chuyển trên d sao cho MC > MD và ở ngoài O qua M kẻ 2 tiếp tuyến MA , MB . Gọi H là trung điểm của CD và giao điểm của AB với MO , với OH lần lượt là E, F . Đoạn thẳng OM cắt cung nhỏ tại I
✿ CMR : OM VUÔNG GÓC AB , OH.OF=OE.OM
Cho (O,R), M nằm ngoài (O). Qua M kẻ tiếp tuyến MA, MB và cát tuyến MCD qua O, AB cắt CD tại H.
a) Chứng minh MA^2=MD.MC
b) Chứng minh MH.MO=MC.MD và C là tâm đường tròn nội tiếp tam giác MAB
c) Giả sử điểm M thay đổi ở ngoài (O) nhưng luôn thuộc đường thẳng d cố định. Chứng minh điểm H luôn thuộc 1 đường tròn cố định
a, Xét tam giác MAD và tam giác MCA có
^M _ chung
^MDA = ^MAC ( cùng chắn cung CA )
Vậy tam giác MAD ~ tam giác MCA (g.g)
\(\dfrac{MA}{MC}=\dfrac{MD}{MA}\Rightarrow MA^2=MD.MC\)(1)
b, Vì MA là tiếp tuyến đường tròn (O) với A tiếp điểm
Lại có OA = OB = R ; MA = MB ( tc tiếp tuyến cắt nhau )
=> OM là trung trực đoạn BA
Xét tam giác MAO đường cao AH ta có
\(MA^2=MO.MH\)(2)
Từ (1) ; (2) suy ra \(MO.MH=MD.MC\)
toán hình
Lớp 9:
Từ điểm m ở ngoài đường tròn (o) , vẽ hai tiếp tuyến ma và mb có a với b là hai tiếp điểm, vẽ cát tuyến Mcd không đi qua tâm (o) ( M,C,D theo thứ tự ấy), vẽ tại oe vuông với cd tại e .
a) Chứng minh 5 điểm A,e,o,b,m cùng thuộc một đường tròn.
b) Vẽ cf // am (f thuộc ae ), cd cắt ab tại i . Chứng minh góc aem = góc bem và tam giác efc đồng dạng tam giác ebi .
c) Chứng minh fi // ac.
a) Ta có: \(\angle OEM=\angle OAM=90\Rightarrow OEAM\) nội tiếp
Ta có: \(\angle OAM+\angle OBM=90+90=180\Rightarrow OAMB\) nội tiếp
\(\Rightarrow O,E,A,M,B\) cùng thuộc 1 đường tròn
b) MAEB nội tiếp \(\Rightarrow\angle AEM=\angle ABM=\angle MAB=\angle BEM\)
Vì \(CF\parallel MA\) \(\Rightarrow\angle ECF=\angle EMA=\angle EBA\) (MAEB nội tiếp)
Xét \(\Delta EFC\) và \(\Delta EIB:\) Ta có: \(\left\{{}\begin{matrix}\angle EBI=\angle ECF\\\angle BEI=\angle CEF\end{matrix}\right.\)
\(\Rightarrow\Delta EFC\sim\Delta EIB\left(g-g\right)\)
c) \(\Delta EFC\sim\Delta EIB\Rightarrow\dfrac{EI}{EF}=\dfrac{EB}{EC}\left(1\right)\)
Ta có: \(\angle ECA=\angle ECF+\angle ACF=\angle EBI+\angle MAC=\angle EBI+\angle CBA\)
\(=\angle EBC\)
Xét \(\Delta ECA\) và \(\Delta EBC:\) Ta có: \(\left\{{}\begin{matrix}\angle CEB=\angle CEA\\\angle CBE=\angle ACE\end{matrix}\right.\)
\(\Rightarrow\Delta ECA\sim\Delta EBC\left(g-g\right)\Rightarrow\dfrac{EB}{EC}=\dfrac{EC}{EA}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{EI}{EF}=\dfrac{EC}{EA}\Rightarrow\dfrac{EI}{EC}=\dfrac{EF}{EA}\Rightarrow\) \(FI\parallel AC\)
qua một điểm M ở ngoài dg tròn (O) kẻ cát tuyến MAB , MCD theo thứ tự đó biết sd cung AB bằng 40 độ số đo cung BD bằng 80 độ tính M
Cho đường tròn (O), Alà 1 điểm cố định trên (O) và M là 1 điểm di động trên (O). Qua M vẽ đường vuông góc MH với tiếp tuyến MT với (O).
CMR trong trường hợp tồn tại tam giác OMH thì tia phân giác ngoài ở đỉnh M của tam giác đi qua 1 điểm cố định
Từ một điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MB,MD với (O) (B,D là tiếp điểm ) và một cát tuyến qua M cắt đường tròn tại hai điểm phân biệt A,C.
a)Chứng minh AB.CD=BC.AD
b)Gọi (d) là đường thẳng qua D và song song với MB:(d) cắt BA,BC lần lượt tại I;J.
Chứng minh DI=DJ
giúp với câu b)
b, tam giác MCB ~ tam giác MBA (g.g) => BC/BA =MC/MD (vì MB=MD <= t/c 2 tiếp tuyến cắt nhau) (1)
tam giác MCD ~ tam giác MDA (g.g) => MC/MD= DC/AD (2)
Từ (1),(2) => BC/BA = DC/AD => BC.AD = DC.AB (đpcm)
:Cho hai đường tròn (O,R) và (O',R') ở ngoài nhau (R>R').Trên cùng nữa mặt phẳng bờ OO' vẽ tiếp tuyến chung ngoài MN \(M\in\left(O\right)N\in\left(O'\right)\).Gọi P là điểm đối xứng của M qua OO' .Đừng thẳng PN cắt (O) ở E và (O') ở F.CM PE=NF
cho đường tròn tâm O và một điểm M nằm ngoài đường tròn . Qua M vẽ các tiếp tuyến MA,MB với đường tròn tâm O . Biết \(\widehat{AMB}\) = 54 độ . Hỏi 2 bán kính OA,OB tạo thành góc ở tâm \(\widehat{AOB}\) bằng bao nhiêu độ
Hình bạn tự vẽ nhé :
Xét tứ giác OAMB có : góc AOB + góc OAM + góc AMB +góc OBM =360 độ
⇒ góc AOB + 90 độ +54 độ +90 độ =360 độ
⇒ góc AOB =360 độ - 90 độ -90 độ -54 độ = 126 độ
Dạng phát biểu khác của tiên đề Ơ clit là:
Qua một điểm ở ngoài một đường thẳng có vô số đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng có một đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng có ít nhất một đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
B. Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Cho đường tròn (O; R) và một điểm M cố định nằm ngoài đường tròn (O). Từ M kẻ các tiếp tuyến MA, MB tới (O) (A, B là các tiếp điểm). MO cắt AB tại H. Một đường thẳng d thay đổi đi qua M nhưng không đi qua O cắt đường tròn (O) tại hai điểm N, P (N nằm giữa M và P). Gọi I là trung điểm của NP.
a) Chứng minh bốn điểm M, A, I, O cùng thuộc một đường tròn.
b) Qua B kẻ đường thẳng song song với MO và cắt đường tròn (O) tại D. Chứng minh ![]() và AD là đường kính của (O).
và AD là đường kính của (O).
c) Tiếp tuyến của (O) tại N và P cắt nhau tại F. Chứng minh ![]() đồng dạng
đồng dạng ![]() và điểm F chuyển động trên một đường thẳng cố định khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài.
và điểm F chuyển động trên một đường thẳng cố định khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài.
Câu a),b) tự làm nhé , mình chỉ giúp câu c) thôi .
OI vuông góc NP ( Do I là trung điểm của MP ) , OF vuông góc NP ( Do OF là đường trung trực của NP )
=> O,I,F thẳng hàng
Tam giác ONF vuông tại N , đường cao NI
=> ON^2 = OI.OF
Mà ON=OA
OA^2 = OH.OM
=> OH.OM=OI.OF
=> OH/OI=OF/OM
Xét tam giác OIM và tam giác OHF có
góc MOF chung
OH/OI=OF/OM
=> Tam giác OIM đồng dạng tam giác OHF
=> góc OHF=góc OIM (=90 độ )
OH vuông HF
mà OH vuông AB
=> A,B,F thẳng hàng
=> F nằm trên đường thẳng cố định AB khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài
Điều phải chứng minh