toán hình
Lớp 9:
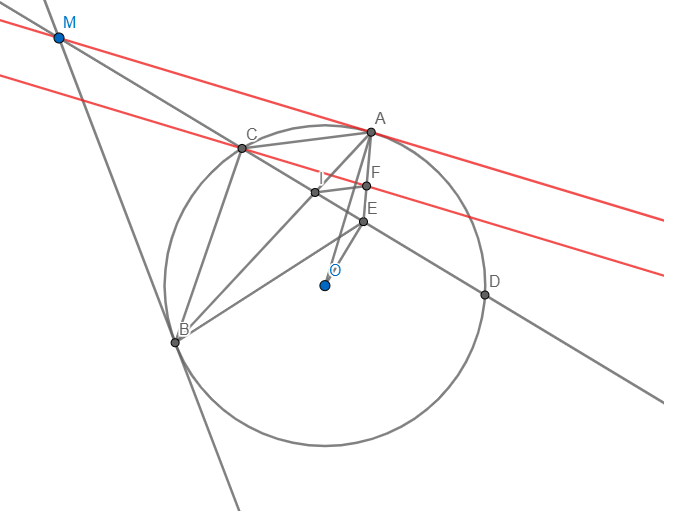
Từ điểm m ở ngoài đường tròn (o) , vẽ hai tiếp tuyến ma và mb có a với b là hai tiếp điểm, vẽ cát tuyến Mcd không đi qua tâm (o) ( M,C,D theo thứ tự ấy), vẽ tại oe vuông với cd tại e .
a) Chứng minh 5 điểm A,e,o,b,m cùng thuộc một đường tròn.
b) Vẽ cf // am (f thuộc ae ), cd cắt ab tại i . Chứng minh góc aem = góc bem và tam giác efc đồng dạng tam giác ebi .
c) Chứng minh fi // ac.
a) Ta có: \(\angle OEM=\angle OAM=90\Rightarrow OEAM\) nội tiếp
Ta có: \(\angle OAM+\angle OBM=90+90=180\Rightarrow OAMB\) nội tiếp
\(\Rightarrow O,E,A,M,B\) cùng thuộc 1 đường tròn
b) MAEB nội tiếp \(\Rightarrow\angle AEM=\angle ABM=\angle MAB=\angle BEM\)
Vì \(CF\parallel MA\) \(\Rightarrow\angle ECF=\angle EMA=\angle EBA\) (MAEB nội tiếp)
Xét \(\Delta EFC\) và \(\Delta EIB:\) Ta có: \(\left\{{}\begin{matrix}\angle EBI=\angle ECF\\\angle BEI=\angle CEF\end{matrix}\right.\)
\(\Rightarrow\Delta EFC\sim\Delta EIB\left(g-g\right)\)
c) \(\Delta EFC\sim\Delta EIB\Rightarrow\dfrac{EI}{EF}=\dfrac{EB}{EC}\left(1\right)\)
Ta có: \(\angle ECA=\angle ECF+\angle ACF=\angle EBI+\angle MAC=\angle EBI+\angle CBA\)
\(=\angle EBC\)
Xét \(\Delta ECA\) và \(\Delta EBC:\) Ta có: \(\left\{{}\begin{matrix}\angle CEB=\angle CEA\\\angle CBE=\angle ACE\end{matrix}\right.\)
\(\Rightarrow\Delta ECA\sim\Delta EBC\left(g-g\right)\Rightarrow\dfrac{EB}{EC}=\dfrac{EC}{EA}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{EI}{EF}=\dfrac{EC}{EA}\Rightarrow\dfrac{EI}{EC}=\dfrac{EF}{EA}\Rightarrow\) \(FI\parallel AC\)