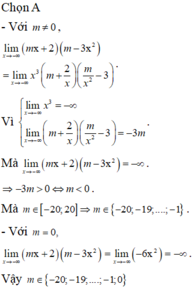có bao nhiêu giá trị m nguyên thuộc đoạn \(\left[-20;20\right]\) để \(\lim\limits_{x\rightarrow-\infty}\left(mx+2\right)\left(m-3x^2\right)=-\infty\)?

Những câu hỏi liên quan
Có bao nhiêu giá trị m nguyên thuộc đoạn [-20; 20] để
lim
x
→
-
∞
(
m
x
+
2
)
(
m
-
3
x
2
)
-
∞
A. 21 B. 22 C. 20 D. 41
Đọc tiếp
Có bao nhiêu giá trị m nguyên thuộc đoạn [-20; 20] để lim x → - ∞ ( m x + 2 ) ( m - 3 x 2 ) = - ∞
A. 21
B. 22
C. 20
D. 41
có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[-3;3\right]\)
để hàm số f(x) = (m+10x + m-2 đồng biến trên R
Lời giải:
Để hàm đồng biến trên $R$ thì:
$m+1>0$
$\Leftrightarrow m>-1$
Mà $m$ nguyên và $m\in [-3;3]$ nên $m\in\left\{0;1;2;3\right\}$
Vậy có 4 giá trị thỏa mãn.
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của m để phương trình
m
x
2
+
20
c
o
s
x
20
có đúng hai nghiệm thực phân biệt thuộc đoạn
0
;
π
2
A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của m để phương trình m x 2 + 20 c o s x = 20 có đúng hai nghiệm thực phân biệt thuộc đoạn 0 ; π 2
A. 1
B. 2
C. 3
D. 0
Có tất cả bao nhiêu giá trị nguyên của m để phương trình
m
x
2
+
20
cos
x
20
có đúng hai nghiệm thực phân biệt thuộc đoạn
0
;
π
2
A. 1. B. 2. C. 3. D. 0.
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của m để phương trình m x 2 + 20 cos x = 20 có đúng hai nghiệm thực phân biệt thuộc đoạn 0 ; π 2
A. 1.
B. 2.
C. 3.
D. 0.
Có tất cả bao nhiêu giá trị nguyên của m để phương trình m x 3 + 20 cos x = 20 có đúng hai nghiệm thực phân biệt thuộc đoạn 0 ; π 2 .
A. 1
B. 2
C. 3
D. 0
Đáp án A
Với mọi m phương trình luôn có nghiệm x = 0
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình
mcos4x + 10sin2xcos2x = 15-m có đúng một nghiệm thuộc đoạn \(\left[\dfrac{-\pi}{6};\dfrac{\pi}{6}\right]\)
cho hàm số \(f\left(x\right)=x^3+2x-5^m\). có bao nhiêu giá trị nguyên của m thuộc đoạn [-6;6] để bất phương trình f(f(x)) \(\ge\) x đúng vs mọi x thuộc (2;6)
Ta có: \(f'\left(x\right)=3x^2+2\ge2;\forall x\)
Đặt \(g\left(x\right)=f\left(f\left(x\right)\right)-x\Rightarrow g'\left(x\right)=f'\left(x\right).f'\left(f\left(x\right)\right)-1\ge2.2-1>0;\forall x\)
\(\Rightarrow g\left(x\right)\) đồng biến trên R
\(\Rightarrow\min\limits_{\left[2;6\right]}g\left(x\right)=g\left(2\right)=f\left(f\left(2\right)\right)-2\)
Ta cần tìm m để \(f\left(f\left(2\right)\right)-2\ge0\)
Đặt \(5^m=t\Rightarrow f\left(2\right)=12-t\)
\(\left(1\right)\Leftrightarrow\left(12-t\right)^3+2\left(12-t\right)-t-2\ge0\)
\(\Leftrightarrow\left(10-t\right)\left(t^2-26t+175\right)\ge0\)
\(\Rightarrow t\le10\)
\(\Rightarrow5^m\le10\Rightarrow m\le log_510\)
Đúng 1
Bình luận (0)
Cho hàm số f(x)=\(\left|x^4-4x^3+4x^2+a\right|\). Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;3] sao cho M≤2m
A.3
B.7
C.6
D.5
\(g\left(x\right)=x^4-4x^3+4x^2+a\)
\(g'\left(x\right)=4x^3-12x^2+8x=0\Leftrightarrow4x\left(x^2-3x+2\right)\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
\(f\left(0\right)=f\left(2\right)=\left|a\right|\) ; \(f\left(1\right)=\left|a+1\right|\)
TH1: \(\left\{{}\begin{matrix}M=\left|a\right|\\m=\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\ge\left|a+1\right|\\\left|a\right|\le2\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{2}{3}\le a\le-\dfrac{1}{2}\\a\le-2\end{matrix}\right.\) \(\Rightarrow a=\left\{-3;-2\right\}\)
TH2: \(\left\{{}\begin{matrix}M=\left|a+1\right|\\m=\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a+1\right|\ge\left|a\right|\\\left|a+1\right|\le2\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le a\le-\dfrac{1}{3}\\a\ge1\end{matrix}\right.\) \(\Rightarrow a=\left\{1;2;3\right\}\)
Đúng 1
Bình luận (0)
Cho hàm số f(x) = (x -1)(x -2)...(x -2020). Có bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[-2020;2020\right]\) để phương trình f'(x) = m.f(x) có 2020 nghiệm phân biệt?