Lời giải:
Để hàm đồng biến trên $R$ thì:
$m+1>0$
$\Leftrightarrow m>-1$
Mà $m$ nguyên và $m\in [-3;3]$ nên $m\in\left\{0;1;2;3\right\}$
Vậy có 4 giá trị thỏa mãn.
Lời giải:
Để hàm đồng biến trên $R$ thì:
$m+1>0$
$\Leftrightarrow m>-1$
Mà $m$ nguyên và $m\in [-3;3]$ nên $m\in\left\{0;1;2;3\right\}$
Vậy có 4 giá trị thỏa mãn.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−3; 3] để hàm số f(x) =(m + 1 x + m − 2 đồng biến trên R.
A. 7
B. 5
C. 4
D. 3
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018; 2018] để hàm số y = (m – 2)x + 2m đồng biến trên R.
A. 2015
B. 2017
C. Vô số
D. 2016
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017]để hàm số y = (m − 2)x + 2m đồng biến trên R.
A. 2014
B. 2016
C. Vô số
D. 2015
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017]để hàm số y = ( m 2 − 4)x + 2m đồng biến trên R.
A. 4030
B. 4034
C. Vô số
D. 2015
Có bao nhiêu giá trị nguyên của m thuộc đoạn [0; 3] để hàm số y = ( m 2 − 1)x đồng biến trên R.
A. 0
B. 1
C. 2
D. Kết quả khác
Cho hàm số \(f\left(x\right)=\left|x^2-2x+m\right|\) với \(m\in\left[-2018;2018\right]\). Gọi \(M\) là giá trị nhỏ nhất của hàm số \(f\left(x+\dfrac{1}{x}\right)\) trên tập \(R\backslash\left\{0\right\}\). Số giá trị \(m\) nguyên để \(M\ge2\) là bao nhiêu?
có bao nhiêu giá trị nguyên của m trên (-4;4) để hàm số y=(m+2)x^2-3mx-5 đồng biến trên (3;+∞)
Cho hàm số y=\(\sqrt{1-\left|2x^2+mx+m+15\right|}\). Có bao nhiêu giá trị của tham số m để hàm số xác định trên đoạn [1;3]
Tìm giá trị thực của tham số m để hàm số y = (2m + 1)x + m – 3 đồng biến trên R.
A. ![]()
B. ![]()
C. 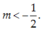
D.