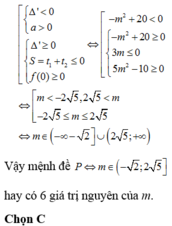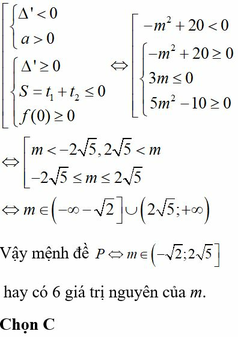Có bao nhiêu giá trị nguyên của tham số m thuộc \(\left[-10;10\right]\) để phương trình: 23m.7\(x^2-2x\) + 73m.2\(x^2-2x\) =143m(7x2 -14x +2 -7.3m) có 4 nghiệm phân biệt trong đó có đúng hai nghiệm lớn hơn -1

Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10; 10] để phương trình m x 2 - m x + 1 = 0 có nghiệm.
A. 17
B. 18
C. 20
D. 21
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[-3;3\right]\)
để hàm số f(x) = (m+10x + m-2 đồng biến trên R
Lời giải:
Để hàm đồng biến trên $R$ thì:
$m+1>0$
$\Leftrightarrow m>-1$
Mà $m$ nguyên và $m\in [-3;3]$ nên $m\in\left\{0;1;2;3\right\}$
Vậy có 4 giá trị thỏa mãn.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( -10; 10) sao cho đồ thị hám số y = \(^{x^3-2mx^2+\left(2m+6\right)x}\) có 2 điểm cực trị nằm về 2 phía khác nhau của trục hoành
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình
mcos4x + 10sin2xcos2x = 15-m có đúng một nghiệm thuộc đoạn \(\left[\dfrac{-\pi}{6};\dfrac{\pi}{6}\right]\)
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;20] để bất phương trình
2
2
x
+
1
-
12
m
.
2
x
-
1
+
5
m
2...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;20] để bất phương trình 2 2 x + 1 - 12 m . 2 x - 1 + 5 m 2 - 10 < 0 có nghiệm thực?
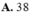
![]()
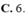
![]()
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn
-
20
;
20
để bất phương trình
2
2
x
+
1
-
12
m
.
2
x
-
1
+...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn - 20 ; 20 để bất phương trình 2 2 x + 1 - 12 m . 2 x - 1 + 5 m 2 - 10 < 0 có nghiệm thực?
A. 38
B. 3
C. 6.
D. 32
có bao nhiêu giá trị nguyên của tham số m trên đoạn \([-2020;2020]\) để phương trình \(\left|\sqrt{4x^2-12x+10}-\sqrt{4x^2+20x+74}\right|=m\) có nghiệm
Đặt \(T=\left|\sqrt{4x^2-12x+10}-\sqrt{4x^2+20x+74}\right|\)
\(T=\left|\sqrt{\left(2x-3\right)^2+1}-\sqrt{\left(2x+5\right)^2+7^2}\right|\)
Trong hệ tọa độ Oxy, xét \(M\left(2x;0\right);A\left(3;1\right);B\left(-5;7\right)\)
Ta có: \(\left\{{}\begin{matrix}AM=\sqrt{\left(2x-3\right)^2+1}\\BM=\sqrt{\left(2x+5\right)^2+7^2}\end{matrix}\right.\) ; \(AB=\sqrt{8^2+6^2}=10\)
\(\Rightarrow T=\left|AM-BM\right|\le AB=10\)
\(\Rightarrow0\le T\le10\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(0\le m\le10\)
Có 11 giá trị nguyên của m thỏa mãn
Đúng 0
Bình luận (0)
a) Tam thức fleft(xright)x^2+2left(m-1right)+m^2-3m+4 không âm với mọi giá trị xb) Có bao nhiêu giá trị nguyên của tham số m để mọi x thuộc R biểu thức fleft(xright)x^2+left(m+2right)x+8m+1 luôn nhận giá trị dươngc) Tìm tất cả các giá trị m để biểu thức fleft(xright)x^2+left(m+1right)x+2m+70forall xin R
Đọc tiếp
a) Tam thức \(f\left(x\right)=x^2+2\left(m-1\right)+m^2-3m+4\) không âm với mọi giá trị x
b) Có bao nhiêu giá trị nguyên của tham số m để mọi x thuộc R biểu thức \(f\left(x\right)=x^2+\left(m+2\right)x+8m+1\) luôn nhận giá trị dương
c) Tìm tất cả các giá trị m để biểu thức \(f\left(x\right)=x^2+\left(m+1\right)x+2m+7>0\forall x\in R\)
có bao nhiêu giá trị nguyên của tham số m thuộc (-8;+vô cực) để phương trình sau có nhiều hơn 2 nghiệm phân biệt : \(x^2+x\left(x-1\right)2^{x+m}+m=\left(2x^2-x+m\right)\cdot2^{x-x^2}\)
Có bao nhiêu giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm f(x)= \(\left|-x^3+2x^2-2x+m+2\right|\) trên đoạn [0;2] không vượt quá 10?
A.25 B.17 C.26 D.18