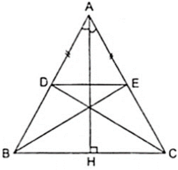
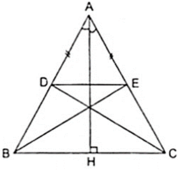
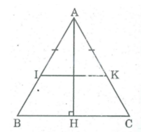
Cho△ABC cân tại A , đường cao AH . Lấy M ∈ cạnh AB ; N ∈ tia đối tia CA sao cho BM = NC . MN cắt BC tại I . Kẻ ND // AB ( D ∈ tia BC )
a) CMR : BMND là hình bình hành
b) Kẻ OI ⊥ MN ( O ∈ tia AH)
CMR : ΔOBM = ΔOCN
c) CMR : OC ⊥ AN
d) CMR : 1/AB2 + 1/OB2 = 4/BC2