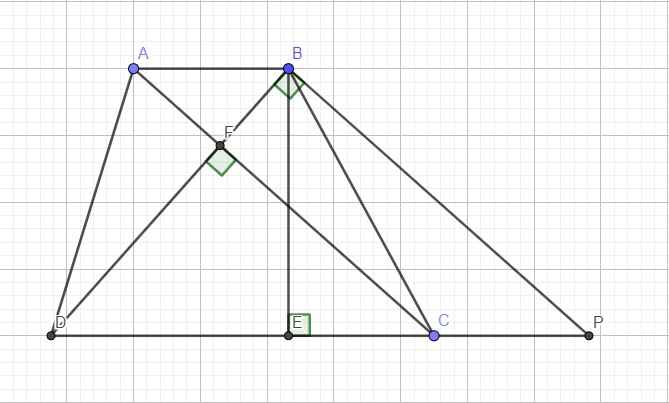
Cho hình thang vuông ABCD có AB=15cm ; DC=20cm ;AD=12cm .TRong hình thang có hình tam giác BMN . Tính diện tích hình tam giác BMN , biết AM=MD và DN=10cm .

Những câu hỏi liên quan
Cho hình thang ABCD có AB//CD, AB<CD, đường chéo BD vuông góc với cạnh BC. Kẻ BH vuông góc với CD. Tính diện tích hình thang ABCD biết BC=15cm, DC= 25cm. (ABCD ko phải hình thang cân)
Cho hình thang vuông ABCD, có ��^widehat{A}, widehat{D} vuông và AB 15cm; AD 20cm, biết AC và BD vuông góc với nhau ở O. Tính diện tích hình thang ABCD
Đọc tiếp
Cho hình thang vuông ABCD, có \(\widehat{A}\), \(\widehat{D}\) vuông và AB = 15cm; AD = 20cm, biết AC và BD vuông góc với nhau ở O. Tính diện tích hình thang ABCD
cho hình thang ABCD (AB//CD) và AB < CD, có BC=15cm, đường cao BH=12 cm, DH=16cm
a) Tính HC
b) CM: DB vuông góc với BC
c) Tính diện tính hình thang ABCD
a)Theo định lý Pytago ta có
HC2=BC2-BH2
HC2=152-122
HC2=81
HC=9 (cm)
b)DC=DH+HC=16+9=25
Áp dụng định lý Pytago đảo ta có
DC2=BD2+BC2
252=202+152
625=625
=>Tam giác BCD vuông tại D
=>BD vuông góc BC
Đúng 0
Bình luận (0)
Cho hình thang ABCD,AB//CD và hai đường chéo vuông góc. BD=15cm, đường cao hình thang là 12cm.Tính diện tích hình thang ABCD
Kẻ đường cao BE \(\Rightarrow BE=12\)
Pitago tam giác vuông BDE:
\(DE=\sqrt{BD^2-BE^2}=9\left(cm\right)\)
Qua B kẻ đường thẳng song song AC cắt CD kéo dài tại P
Do \(AC\perp BD\Rightarrow BP\perp BD\) hay tam giác BPD vuông tại B
Mặt khác \(\left\{{}\begin{matrix}AB||CD\\AC||BP\end{matrix}\right.\) \(\Rightarrow ABPC\) là hbh
\(\Rightarrow AB=CP\Rightarrow AB+CD=CP+CD=DP\)
Hệ thức lượng tam giác vuông BPD:
\(BD^2=DE.DP\Rightarrow DP=\dfrac{BD^2}{DE}=25\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}BE.\left(AB+CD\right)=\dfrac{1}{2}BE.DP=\dfrac{1}{2}.9.25=112,5\left(cm^2\right)\)
Đúng 3
Bình luận (0)
cho hình thang vuông ABCD có góc A=D=90, AB=4cm,AD=15cm,BC=17cm. Tính CD
Cho hình vuông ABCD vuông tại A có AB//CD và AB<CD. Kẻ AH vuông góc với BD tại H. Tính BH và diện tích hình thang ABCD nếu biết BC=13cm, CD=14cm và DB=15cm
Bài 3: Cho hình thang ABCD (đáy AB, CD) 𝐴̂ = 𝐷̂ = 900 có hai đường chéo vuông góc với nhau tại O, AB = 15cm, AD = 20cm.
a) Tính độ dài OB, OD
b) Tính độ dài AC
c) Tính diện tích hình thang ABCD
a: Xét ΔDAB vuông tại A có
\(DB^2=AB^2+AD^2\)
hay DB=25(cm)
Xét ΔDAB vuông tại A có AO là đường cao ứng với cạnh huyền DB
nên \(\left\{{}\begin{matrix}AD^2=DO\cdot DB\\AB^2=BO\cdot BD\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DO=16\left(cm\right)\\OB=9\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(a,BD=\sqrt{AB^2+AD^2}=25\left(cm\right)\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AD^2=OD\cdot BD\\AB^2=OB\cdot BD\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}OD=\dfrac{AD^2}{BD}=16\left(cm\right)\\OB=\dfrac{AB^2}{BD}=9\left(cm\right)\end{matrix}\right.\)
\(b,\) Áp dụng HTL:
\(\left\{{}\begin{matrix}AO^2=DO\cdot OB=144\\AD^2=AO\cdot AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AO=12\left(cm\right)\\AC=\dfrac{AD^2}{AO}=\dfrac{100}{3}\left(cm\right)\end{matrix}\right.\)
\(c,DC=\sqrt{AD^2+AC^2}=\dfrac{20\sqrt{34}}{3}\left(cm\right)\\ S_{ABCD}=\dfrac{1}{2}AD\left(AB+CD\right)=10\left(\dfrac{20\sqrt{34}}{3}+15\right)=\dfrac{450+200\sqrt{34}}{3}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD có AB // DC và AB<DC, đường chéo BD vuông góc với cạnh bên BC. Vẽ đường cao BH
a) Chứng minh △BDC đồng dạng với △HBC
b) Cho BC= 15cm, DC= 25cm. Tính HC và HD
c) Tính diện tích hình thang ABCD
a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng vói ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có AB//DC và AB<DC, đường chéo BD vuông góc với cạnh bên C.Về đường cao BH. a Chứng minh ABDC đồng dạng A HBC b Cho BC=15cm DC=25. Tính HC và HD • Tính diện tích hình thang ABCD.
a:Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng với ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
Đúng 0
Bình luận (0)