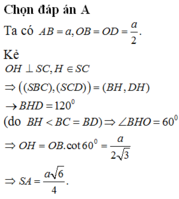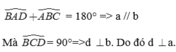Hình bên cho biết ∠BAD1300; ∠ADC500. Chứng tỏ rằng: AB//CD.
A B D C
Đọc tiếp
Hình bên cho biết ∠BAD=1300; ∠ADC=500. Chứng tỏ rằng: AB//CD.
Những câu hỏi liên quan
9 tháng 2 2023 lúc 21:01
Tứ giác ABCD nội tiếp (O).Biết góc BOD =1300 thì số đo góc BAD là
A.1300 B.500 C.650 D.150
\(\widehat{BOD}=130^o\Rightarrow\stackrel\frown{BD}=130^o\\ \widehat{BAD}=\dfrac{1}{2}sđ\stackrel\frown{BD}=\dfrac{1}{2}\times130^o=65^o\\ \Rightarrow C\)
Đúng 1
Bình luận (0)
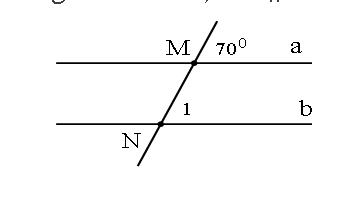
Bài 47: Trong hình vẽ bên, để a // b thì số đo góc N1 bằng:
A. 1100
B. 1000
C. 1300
D. 700
Xem thêm câu trả lời
hình vẽ H1, biết số đo Â1 1300 vậy số đo B1:A. 500 B. 1300 C. 1800 D. 900
Đọc tiếp
hình vẽ H1, biết số đo Â1= 1300 vậy số đo B1:
A. 500 B. 1300 C. 1800 D. 900 
Xem thêm câu trả lời
Cho tứ giác ABCD có E là giao điểm của AB và CD; F là giao điểm của BC và AD. Các tia phân giác của góc E và góc F cắt nhau tại I. Chứng minh: Nếu BAD=1300; BCD = 500 thì IE vuông góc với IF (giải + vẽ hình)
Giúp tui vs bà con ơi!!!!
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
∠
B
A
D
60
0
, cạnh bên SA vuông góc với đáy. Biết rằng góc giữa hai mặt phẳng (SBC) và (SCD) bằng
60
0
Độ dài đoạn thẳng SA bằng A.
a
6
4
B.
a
6...
Đọc tiếp
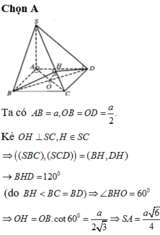
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ∠ B A D = 60 0 , cạnh bên SA vuông góc với đáy. Biết rằng góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 Độ dài đoạn thẳng SA bằng
A. a 6 4
B. a 6 2
C. a 3 2
D. a 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
0
, cạnh bên SA vuông góc với đáy. Biết rằng góc giữa hai mặt phẳng (SBC) và (SCD) bằng
60
0
. Độ dài đoạn thẳng SA bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 0 , cạnh bên SA vuông góc với đáy. Biết rằng góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 . Độ dài đoạn thẳng SA bằng
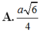
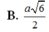
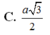
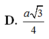
Trong hình bên biết:
B
A
D
^
110°,
A
B
C
^
70°,
B
C
^
D
90°. Chứng minh hai đường thẳng a và d vuông góc với nhau
Đọc tiếp
Trong hình bên biết: B A D ^ = 110°, A B C ^ = 70°, B C ^ D = 90°.
Chứng minh hai đường thẳng a và d vuông góc với nhau
Ta có B A D ^ + A B C ^ = 180° => a // b
Mà B C D ^ = 90°=>d ⊥ b. Do đó d ⊥ a
Đúng 0
Bình luận (0)
Trong hình bên biết:
B
A
D
^
110
°
,
A
B
C
^
70
°
,
B
C
^
D
90
°
.Chứng minh hai đường thẳng a và d vuông góc với nhau.
Đọc tiếp
Trong hình bên biết: B A D ^ = 110 ° , A B C ^ = 70 ° , B C ^ D = 90 ° .
Chứng minh hai đường thẳng a và d vuông góc với nhau.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi với cạnh
a
3
,
B
A
D
^
120
∘
và cạnh bên SA
⊥
(ABCD). Biết số đo của góc giữa hai mặt phẳng (SBC) và (ABCD) bằng
60
∘
. Tính khoảng cách d giữa hai đường thẳng BD và SC.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi với cạnh a 3 , B A D ^ = 120 ∘ và cạnh bên SA ⊥ (ABCD). Biết số đo của góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60 ∘ . Tính khoảng cách d giữa hai đường thẳng BD và SC.
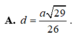
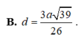
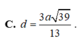
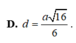
Cho hình chóp S.ABCD có đáy ABCD là hình thoi với cạnh
a
3
;
B
A
D
^
120
o
và cạnh bên SA
⊥
(ABCD). Biết số đo của góc giữa hai mặt phẳng ( SBC ) và ( ABCD ) bằng
60
o
. Tính khoảng cách d giữa hai đường thẳng BD và SC. A.
d...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi với cạnh a 3 ; B A D ^ = 120 o và cạnh bên SA ⊥ (ABCD). Biết số đo của góc giữa hai mặt phẳng ( SBC ) và ( ABCD ) bằng 60 o . Tính khoảng cách d giữa hai đường thẳng BD và SC.
A. d = a 29 26
B. d = 3 a 29 26
C. d = 3 a 39 13
D. d = a 16 6
Gọi O = A C ∩ B D . Ta có
B D ⊥ A C B D ⊥ S C ⇒ B D ⊥ S A C
Kẻ OI ⊥ SC nên OI là đoạn vuông góc chung của BD và SC. Lại có ∆ I C O ~ A C S nên suy ra O I = 3 a 29 26 Vậy d = 3 a 29 26
Đáp án B
Đúng 0
Bình luận (0)