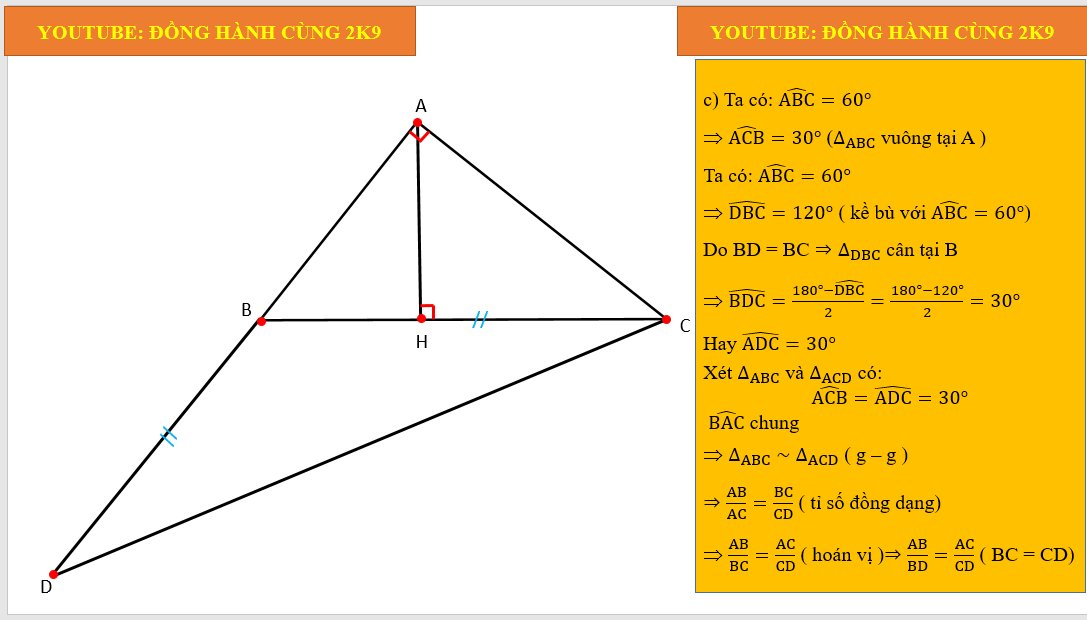
Cho tam giác ABC vuông tại A: AB=8cm:AC=6cm.
A) Tính BC ; So sánh các góc của tam giác ABC
B) Vẽ trung tuyến BM . Trên tia đối của tia MB lấy điểm D sao cho MB=MD.Chứng minh: tam giác ABM= tam giác CDM; từ đó suy ra tam giác MCD vuông
C) Chứng minh DAC > BAD