Cho tam giác ABC có \(\widehat{B}=70\) độ ; \(\widehat{C}=50\) độ . H là trực tâm . O là giao của 3 đường trung trực . M là trung điêm rcuar BC. Lấy D : M là trung điểm của OD . TÍnh \(\widehat{AHD}\) ?

Những câu hỏi liên quan
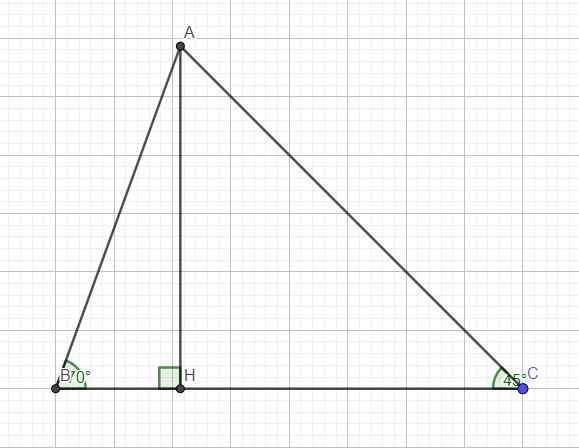
Cho tam giác ABC có BC = 4cm, \(\widehat{B}=70^o\), \(\widehat{C}=45^o\). Tính độ dài AC và diện tích tam giác ABC?
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A có \(\widehat{BAC}\) = 70 độ. Điểm D nằm trong tam giác ABC sao cho DA = DB và \(\widehat{CAD}\) = 65 độ. Tính \(\widehat{BCD}\)
Cho tam giác ABC có \(\widehat{A}\)= 70 độ, \(\widehat{B}\): \(\widehat{C}\)= 2 : 3. So sánh các cạnh của tam giác ABC
#GIÚPMKNHA
Xét tam giác ABC có : A + B + C = 180 độ
mà A = 70 độ => B + C = 110 độ
B : C = 2 : 3 => B/2 = C/3
=> B/2 = C/3 = B + C / 2 + 3 ( áp dụng t.c dãy tỉ số bằng nhau )
=> B/2 = C/3 = 110/5
=> B/2 = C/3 = 22
=> B = 22 . 2 = 44 ( độ )
C = 22 . 3 = 66 ( độ )
Do 44 độ < 66 độ < 70 độ
=> B < C < A
=> AC < AB < BC ( quan hệ cạnh đối diện và góc lớn hơn )
TK mk nha !!!
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
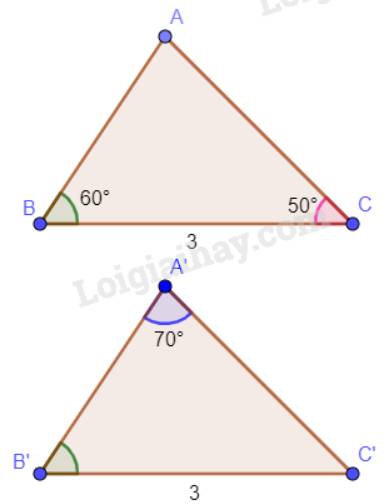
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\). Tính R,b,c.
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\( \Rightarrow R = \dfrac{a}{{2\sin A}};\;\;b = \dfrac{{a.\sin B}}{{\sin A}}\)
Mà \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\)
\( \Rightarrow R = \dfrac{{10}}{{2\sin {{45}^o}}} = 5\sqrt 2 ;\;\;b = \dfrac{{a.\sin {{70}^o}}}{{\sin {{45}^o}}} \approx 13,29\)
Mặt khác: \(\widehat A = {45^o},\widehat B = {70^o} \Rightarrow \widehat C = {65^o}\)
Từ định lí sin ta suy ra: \(c = \dfrac{{a.\sin C}}{{\sin A}} = \dfrac{{10.\sin {{65}^o}}}{{\sin {{45}^o}}} \approx 12,82.\)
Vậy \(R = 5\sqrt 2 ;\;\;b \approx 13,29\); \(c \approx 12,82.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC. Tia phân giác của góc B cắt tia phân giác của góc C tại M. Tính \(\widehat{BMC}\) biết \(\widehat{BAC}\) = 70 độ
Tam giác ABC cân tại A nên ABC = ACB =\(90-\frac{BAC}{2}=90-\frac{70}{2}=90-35=55\)độ
BM, CM lần lượt là phân giác của góc B, góc C nên CBM = BCM =\(\frac{1}{2}ABC\left(=\frac{1}{2}ACB\right)\)\(\frac{55}{2}\)độ
Tam giác BCM có: BCM + CBM + BMC = 180 độ \(\Rightarrow\)\(2\times\frac{55}{2}\)+ BMC = 180 độ
Góc BMC = 180 -55= 125 độ
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(\widehat {ABC} = \widehat {DEF} = {70^\circ },\widehat {BAC} = \widehat {EDF} = {60^\circ },AC = 6\;{\rm{cm}}.\)
Tính độ dài cạnh DF.
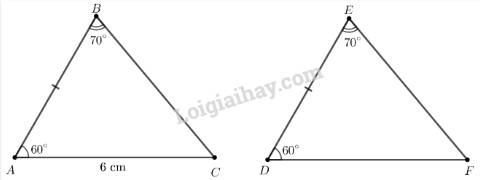
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}\widehat {ABC} = \widehat {DEF} (= {70^\circ })\\AB = DE\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\( \Rightarrow \Delta ABC{\rm{ = }}\Delta DEF\)(g.c.g)
\( \Rightarrow DF = AC\)( 2 cạnh tương ứng)
Mà AC = 6 cm
\( \Rightarrow DF = 6cm\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{A}=180^o-3\times\widehat{C}\); \(\widehat{B}=70^o\)
Vẽ tia phân giác \(\widehat{B}\) cắt AC tại E. Qua E kẻ đường thẳng song song BC cắt AB tại D.CMR: ED là tia phân giác của \(\widehat{AED}\)
Ta có \(\widehat{A}+\widehat{ABC}+\widehat{C}=180^0\Rightarrow180^0-3\widehat{C}+\widehat{C}=180^0-70^0=110^0\)
\(\Rightarrow2\widehat{C}=70^0\Rightarrow\widehat{C}=35^0\Rightarrow\widehat{A}=180^0-3\cdot35^0=75^0\)
Ta có BE là p/g nên \(\widehat{B_1}=\widehat{B_2}=\dfrac{1}{2}\widehat{ABC}=35^0\)
Mà \(ED//BC\) nên \(\widehat{B_2}=\widehat{E_2}=35^0\left(so.le.trong\right)\left(1\right)\)
Ta có \(ED//BC\Rightarrow\widehat{E_1}=\widehat{C}=35^0\left(đồng.vị\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\widehat{E_1}=\widehat{E_2}\left(=35^0\right)\)
Vậy ...
Đúng 2
Bình luận (0)
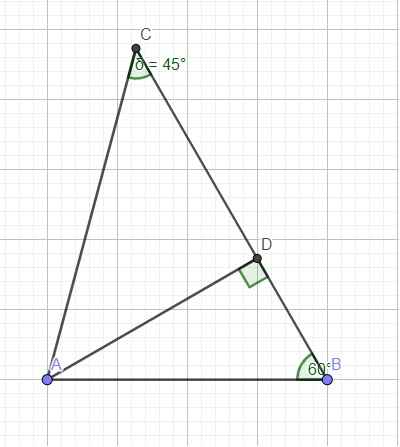
Cho tam giác ABC có góc A = 75 độ, AB = 10,6 cm, \(\widehat{B}\) : \(\widehat{C}\) = 4:3. Tính CA, CB và diện tích tam giác ABC
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
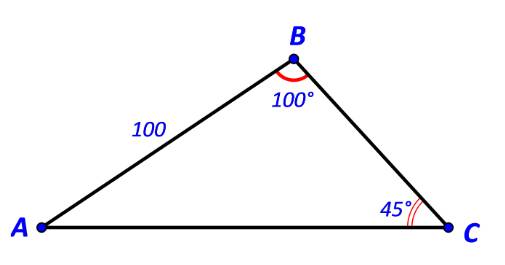
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
Đúng 0
Bình luận (0)