Cho ham số y=\(\sqrt{x^2}-2\)
a. vẽ ĐTHS (T) của hàm số trên
b.Viết ptđt (d') đi qua M(x=t-2;y=3t+5) vơi t thuộc R
c. Giao điểm của T và D'
Câu 1: hàm số \(y=\sqrt{2}\).Chọn kết luận đúng
A. Đths không cắt trục Ox
B. Đths đi qua điểm \((1;\sqrt{2})\)
C. Hs đồng biến trên toàn trục số
D. Hs nghịch biến trên\((-\infty;0) \)
Câu 2: Cho pt \(y=|x|+2x\). Chọn kết luận đúng
A.Đths đi qua điểm\((1;2)\)
B.Đths không cắt trục Ox
C.Hs nghịch biến trên\((-\infty;0) \)
D.Hs đồng biến trên toàn trục số
Câu 3: Cho 1 tam giác vuông với độ dài các cạnh được tính theo đơn vị là cm. Nếu tăng các cạnh góc vuông lên 2cm và 3cm thì S tam giác ban đầu tăng lên 50\(cm^2\) . Nếu giảm cả hai cạnh góc vuông đi 2cm thì S tam giác ban đầu giảm đi 32\(cm^2\). Tích hai cạnh góc vuông của tam giác ban đầu là
A. 208\(cm^2\) B.36\(cm^2\) C.32\(cm^2\) D.34\(cm^2\)
Câu 4: Cho hình vuông ABCD có độ dài cạnh bằng a. Hai điểm M và N lần lượt là trung điểm của BC và CD. Tích vô hướng \(\overrightarrow{AM}.\overrightarrow{AN}\)=?
Câu 5: Đths \(y=-x+2m+1\) tạo với các trục tọa độ 1 tam giác có S=18. Tính giá trị của m
Câu 6: Phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm âm phân biệt \(x_1,x_2\). Khi đó mệnh đề nào sau đây sai?
A. Parabol \(y=ax^2+bx+c\) cắt trục hoành tại hai điểm phân biệt
B. Phương trình \(cx^2+bx+a=0\) có hai nghiệm phân biệt \(\frac{1}{x_1}, \frac{1}{x_2}\)
C. Đỉnh của parabol \(y=ax^2+bx+c\) nằm ở phía bên phải trục tung
D. Biểu thức \(ax^2+bx+c\) có thể viết dưới dạng \(a(x-x_1)(x-x_2)\)
1.
Vì \(y=\sqrt{2}\) là hàm hằng nên với mọi giá trị của \(x\) thì đều nhận \(\sqrt{2}\) là giá rị của \(y\)
\(\Rightarrow B\)
2. \(D\)
3.
Giải hệ \(\left\{{}\begin{matrix}\dfrac{1}{2}\left(x+2\right)\left(y+3\right)=\dfrac{1}{2}xy+50\\\dfrac{1}{2}\left(x-2\right)\left(y-2\right)=\dfrac{1}{2}xy-32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=26\\y=8\end{matrix}\right.\)
\(\Rightarrow xy=208\Rightarrow A\)
4.
\(\overrightarrow{AM}.\overrightarrow{AN}=-a^2\)
5.
\(\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)
6. \(C\)
cho hàm số y=f(x)=(2.a+3).x tìm a biết ĐTHS đi qua điểm A(1;4). Vẽ ĐTHS vừa tìm được
Câu 1: Cho hàm số y=(m-1)x+2m
a) Xác định m để đồ thị hàm số đi qua 2 điểm M(-1;-2)
b) Vẽ đths trên khi m=-1
a: Thay x=-1 và y=-2 vào y=(m-1)x+2m, ta được:
\(-\left(m-1\right)+2m=-2\)
=>2m-m+1=-2
=>m+1=-2
=>m=-3
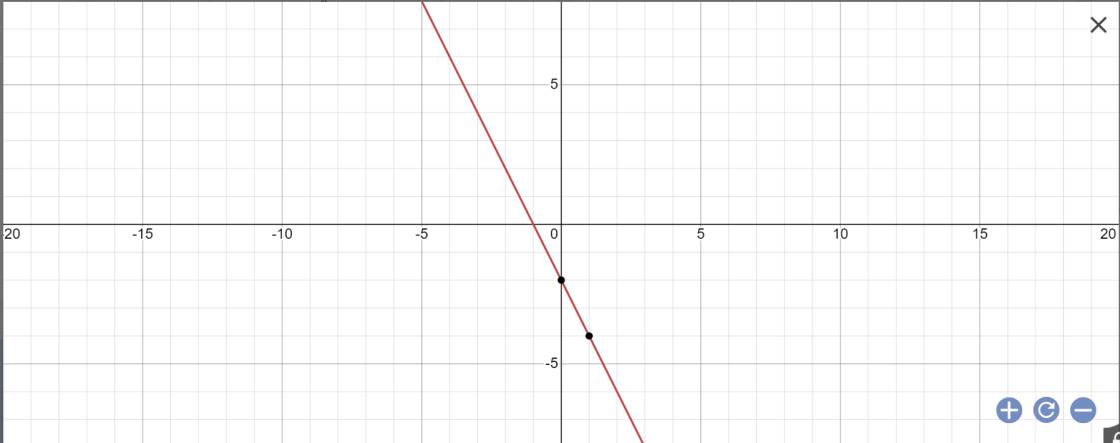
b: Khi m=-1 thì \(y=\left(-1-1\right)x+2\cdot\left(-1\right)=-2x-2\)
1. Cho hàm số \(y=\dfrac{3x^2+13x+19}{x+3}\). Đường thẳng đi qua 2 điểm cực trị của đths có phương trình là:
\(A.5x-2y+13=0\)
\(B.y=3x+13\)
\(C.y=6x+13\)
\(D.2x+4y-1=0\)
2. Cho hàm số \(y=\sqrt{x^2-2x}\). Khẳng định nào sau đây là đúng?
A. Hàm số có 2 điểm cực trị
B. Hàm số đạt cực tiểu tại x=0
C. Hàm số đại cực đại tại x=2
D. Hàm số có đúng 4 điểm cực trị
3. Cho hàm số \(y=x^7-x^5\). Khẳng định nào sau đây đúng?
A. Hàm số có đúng 1 điểm cực trị
B. Hàm số có đúng 3 điểm cực trị
C. Hàm số có đúng 2 điểm cực trị
D. Hàm số có đúng 4 điểm cực trị
4. Cho hàm số \(y=f\left(x\right)\)có đạo hàm \(f'\left(x\right)=\left(x+1\right)\left(x-2\right)^2\left(x-3\right)^3\left(x+5\right)^4\)
. Hàm số \(y=f\left(x\right)\) có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 4
D. 5
5. Cho hàm số \(y=\left(x^2-2x\right)^{\dfrac{1}{3}}\) . Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x=1
B. Hàm số đạt cực đại tại x=1
C. Hàm số không có điểm cực trị
D. Hàm số có đúng 2 điểm cực trị
Cho đường tròn (C): (x-1)2 + (y+2)2 =9 ; điểm M(1;2) điểm N (3;6) , đường thẳng △:4x - y +5 =0
a) xác định tâm và R của đtr (C)
b) viết ptđt △' qua M và // △
c) viết pttt của (C)
d) viết pt đường tròn (C') tâm M và đi qua N
e) tính d(M,△)
f) viết ptđt d đi qua M và cắt (C) tại 2 điểm A,B sao cho AB=2\(\sqrt{6}\) , AB=4
giúp nhanh với ạ ! :((
c) viết pttt của (C) và _|_ với △ ( sửa đề )
Cho hàm số y = (2m - 3)x - 1 với (m#1/3) (d)
a) Tìm m để hs đồng biến
b) tìm m để (d) đi qua E ( -2; -3) . Vẽ ĐTHS với m vừa tìm được
c) Tìm m sao cho khoảng cách từ gốc toạ độ đến (d) = \(\dfrac{1}{\sqrt{5}}\)
a: Để hàm số đồng biến thì 2m-3>0
hay m>3/2
b: Thay x=-2 và y=-3 vào y=(2m-3)x-1, ta được:
-2(2m-3)-1=-3
=>-2(2m-1)=-2
=>2m-1=1
hay m=1
cho hàm số y=ax
a) xác định a biết ĐTHS đi qua điểm A(-2/3; 2)
b) vẽ ĐTHS với a vừa tìm đc
c) trong các điểm sau, điểm nào thuộc ĐTHS, điểm nào ko thuộc ĐTHS ? : B(-1; 3) , C(1; 3) , D(-1/6; 0,5)
d) xác định tọa độ của điểm thuộc ĐTHS biết giá trị hoành độ là -1/3
e) xác định tọa độ của điểm thuộc ĐTHS biết giá trị tung độ là-2/5
Cho h/s y=ax+b(a khác 0)
a)XĐ hàm số biết đi qua nó song song y=2x-3 và đi qua A(1;-2)
b)Xét h/s biết nó đi qua 2 đ A(1;-2) và B(2;3)
c)Tìm m để đths y=(2m-3)x+2 vuông góc đths vừa tìm đc ở câu b)
a) Vì hàm số y=ax+b song song với y=2x-3 nên a=2
Vậy: y=2x+b
Thay x=1 và y=-2 vào y=2x+b, ta được:
\(2\cdot1+b=-2\)
hay b=-4
Vậy: y=2x-4
b) Vì y=ax+b đi qua A(1;-2) và B(2;3) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=-2\\2a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=-5\\a+b=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=5\\b+5=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=-7\end{matrix}\right.\)
Vậy: y=5x-7
cho hàm số bậc nhất y= (m-1) x +2m
a, tìm m để hàm số đồng biến, nghịch biến
b, tìm m để đồ thị hàm số đi qua điểm A(1;2)
c, vẽ đths khi m=2. Tính chu vi và diện tích tam giác tạo bởi đths với 2 trục tọa độ
d, xác định giao điểm của đths trên trục hoanh và trục tung. Tìm M để diện tích tam giác tạo bởi đths với 2 trục tọa độ bằng 8
e, Tìm m để khoảng cách từ gốc tọa độ đến đths trên đạt giá trị lớn nhất
giúp mk mai kiểm tra rồi. thanks nha!