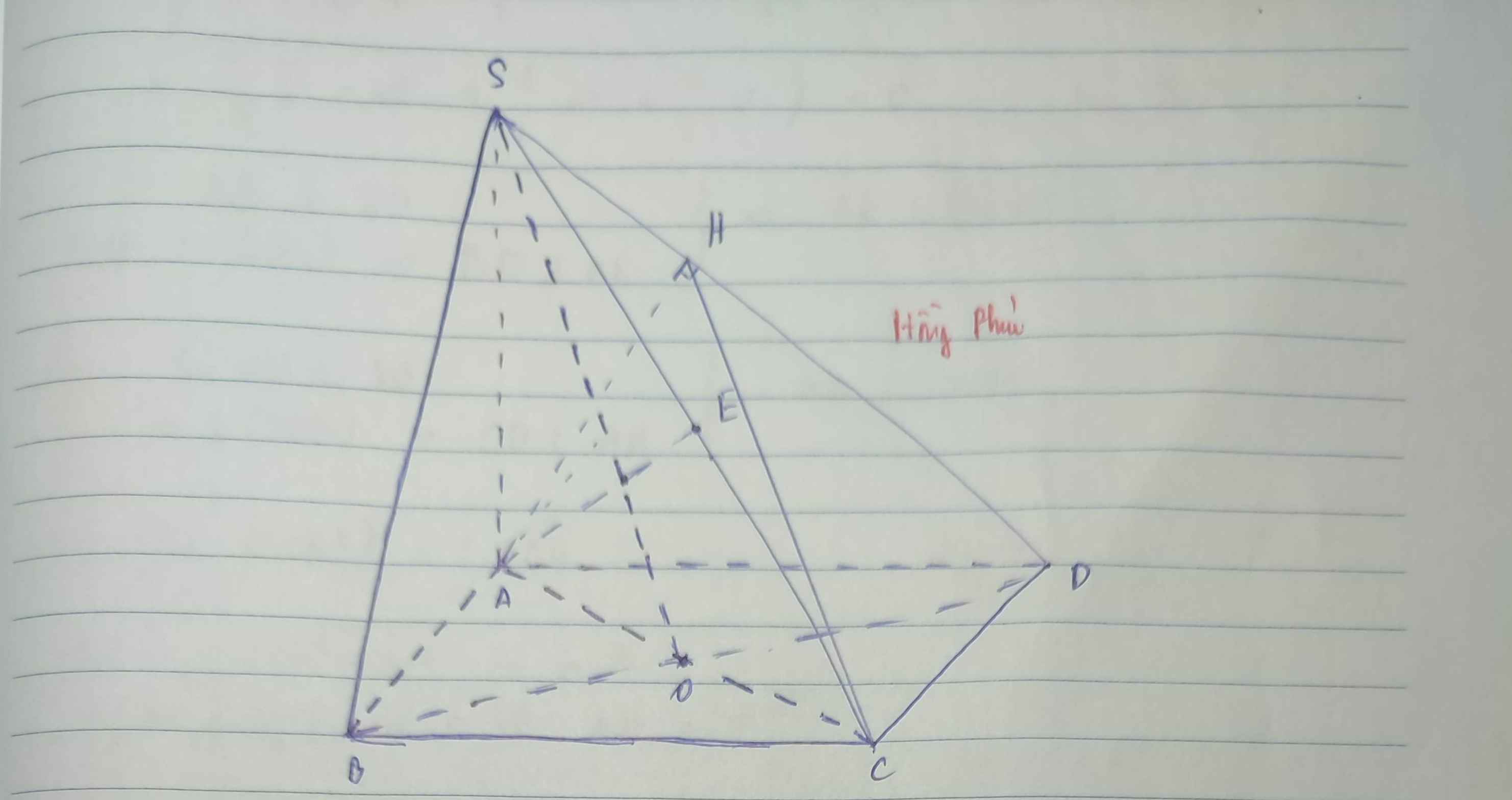
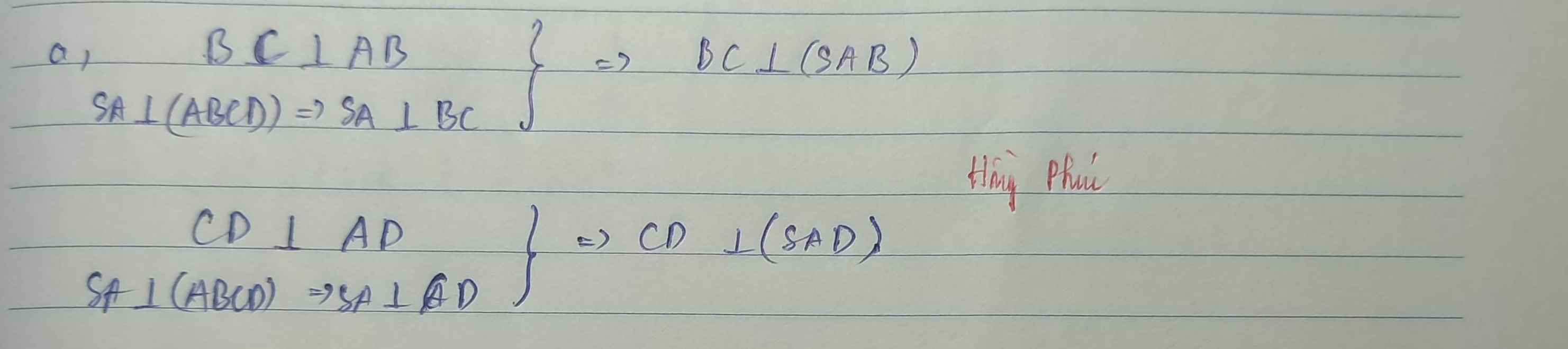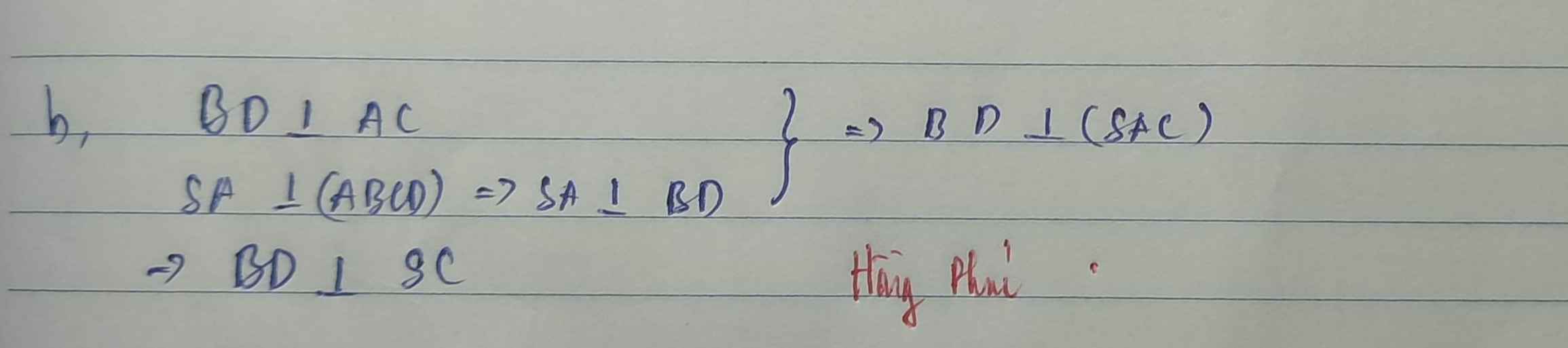giúp em câu c,d với ạ!
giúp em câu c,d với ạ!

Những câu hỏi liên quan
Giúp em với và cảm ơn ạ. Em cần giúp câu b, c, d ạ
giúp em bài 1 câu c câu d với ạ!!!

`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`
Đúng 1
Bình luận (3)
c) Ta có: \(C=\sqrt{\dfrac{3\sqrt{5}+1}{2\sqrt{5}-3}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{\left(3\sqrt{5}+1\right)\left(2\sqrt{5}-3\right)}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{30-9\sqrt{5}+2\sqrt{5}-3}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{27-7\sqrt{5}}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{54-14\sqrt{5}}}{2\sqrt{10}-3\sqrt{2}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\left(7-\sqrt{5}\right)\cdot\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{2}\cdot\left(2\sqrt{5}-3\right)}\)
\(=\dfrac{7\sqrt{5}-7-5+\sqrt{5}}{2\sqrt{5}-3}\)
\(=\dfrac{8\sqrt{5}-12}{2\sqrt{5}-3}\)
\(=\dfrac{4\left(2\sqrt{5}-3\right)}{2\sqrt{5}-3}=4\)
Đúng 0
Bình luận (0)
giúp em câu c,d với ạ em cảm ơn!!!
Đọc tiếp
giúp em câu c,d với ạ em cảm ơn!!!
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
Giúp em câu c,d với ạ
c: Xét ΔBDA vuông tại D và ΔBFC vuông tại F có
\(\widehat{DBA}\) chung
Do đó: ΔBDA\(\sim\)ΔBFC
Suy ra: BD/BF=BA/BC
hay BD/BA=BF/BC
Xét ΔBDF và ΔBAC có
BD/BA=BF/BC
\(\widehat{FBD}\) chung
Do đó: ΔBDF\(\sim\)ΔBAC
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
Suy ra: AE/AF=AB/AC
hay AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AF=AB/AC
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC
Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
\(\widehat{DCA}\) chung
Do đó: ΔCEB\(\sim\)ΔCDA
Suy ra: CE/CD=CB/CA
hay CE/CB=CD/CA
Xét ΔCED và ΔCBA có
CE/CB=CD/CA
\(\widehat{ECD}\) chung
Do đó: ΔCED\(\sim\)ΔCBA
Đúng 1
Bình luận (0)
Mọi người giúp em câu c bài 3 với câu c,d bài 4 với ạ 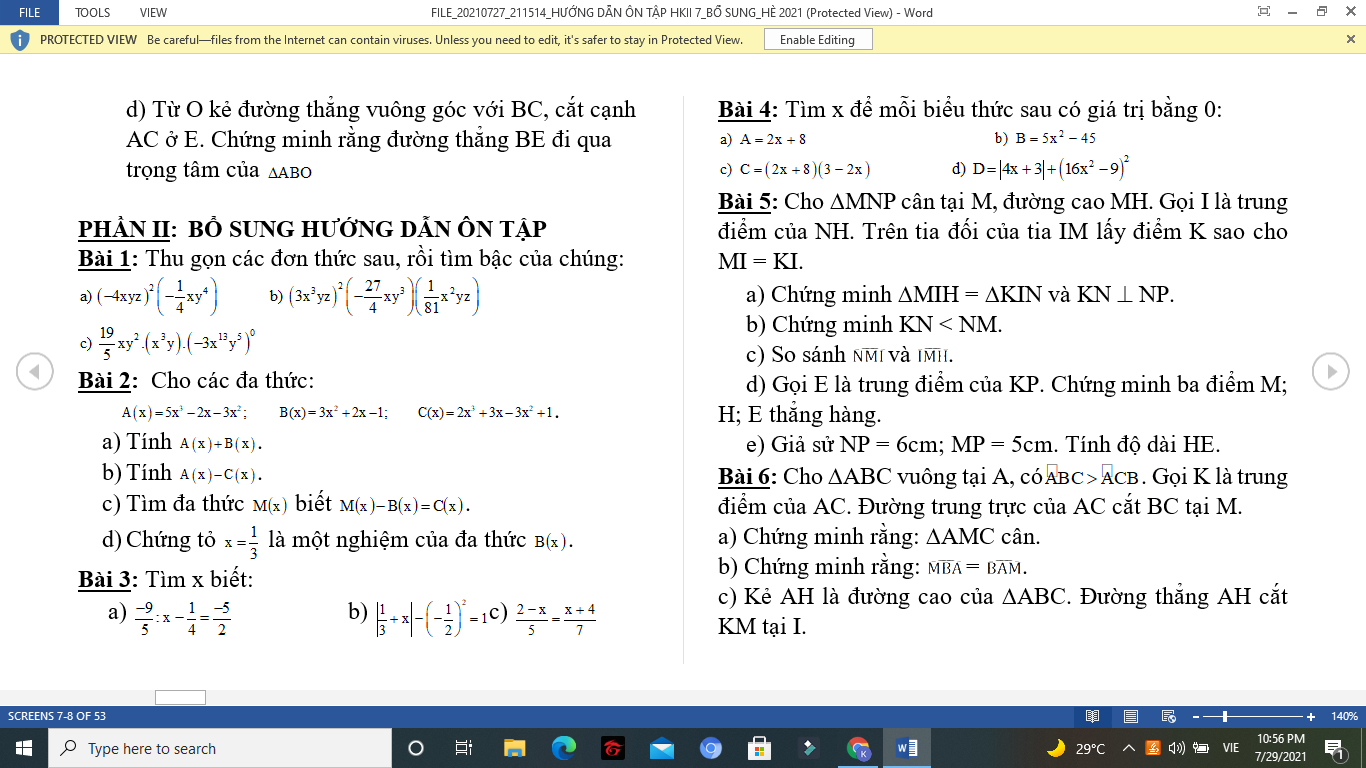
Bài 3:
c) Ta có: \(\dfrac{2-x}{5}=\dfrac{x+4}{7}\)
\(\Leftrightarrow14-7x=5x+20\)
\(\Leftrightarrow-7x-5x=20-14\)
\(\Leftrightarrow-12x=6\)
hay \(x=-\dfrac{1}{2}\)
Đúng 0
Bình luận (0)

giúp em câu c và d với ạ
Giúp em với ạ câu C,D,E
c) 108(12 + 13 ) + 25 . 92
= 2700 + 2300
= 5000
d) 2.169.12 - 3.68.8 - 24
= ( 2 .12 ) . 169 - (3.8) . 68 - 24
= 24 . 169 - 24 . 68 - 24
= 24(169 - 68 ) - 24
= 2424 - 24 = 2400
e) 2.56.24 - 3.36.16 + 4.12.95 + 6.3.8.5
= ( 2 . 24 ) . 56 - ( 3.16 ) . 36 + (4.12) .95 + (6.8) . 3 . 5
= 48 . 56 - 48 . 36 + 48 . 95 + 48 . 15
= 48(56 - 36 + 95 + 15 )
= 6240
Đúng 0
Bình luận (0)
c) 108.12+25.92+13.108
=(108+12)+(25.13)+(108+92)
=120+325+200
=645
Đúng 0
Bình luận (0)
Làm giúp em bài 1 câu (c) và câu (d) với ạ 
Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.Lời giải câu a,b,c của em:
Đọc tiếp

Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.
Lời giải câu a,b,c của em:
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
Đúng 0
Bình luận (0)