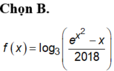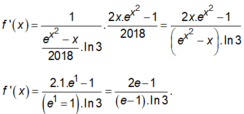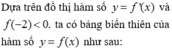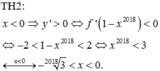Cho x+y=2. CM rằng x2017+y2017\(\le\)x2018+y2018

Những câu hỏi liên quan
Cmr nếu x/y=z/t thì [(x-y)/(z-t)]2017=(x2017+y2017)/(z2017+t2017)
x2019-2019.x2018+2019.x2018+2019.x2017-2019.x2016+......2019.x-200
Tại x=2018
Giúp mik vs nhé mai mik học rồi
x2019-2019.x2018+2019.x2018+2019.x2017-2019.x2016+......2019.x-200
Tại x=2018
Giúp mik vs nhé
frac{^{x1}}{x2}frac{x3}{x2}frac{x3}{x4}....................................frac{x2017}{x2018}va frac{a1}{a2018} ^{5^{ }2017}biet x2+x3+x4+......................+x2018ne0tinh Sfrac{x1+x2+x3+.....................+x2017}{x2+x3+x4+.....................+x2018}
Đọc tiếp
\(\frac{^{x1}}{x2}\)=\(\frac{x3}{x2}\)=\(\frac{x3}{x4}\)=....................................=\(\frac{x2017}{x2018}\)
va \(\frac{a1}{a2018}\)= \(^{5^{ }2017}\)
biet \(x2+x3+x4+......................+x2018\ne0\)
tinh S=\(\frac{x1+x2+x3+.....................+x2017}{x2+x3+x4+.....................+x2018}\)
Cho các số x, y thỏa mãn điều kiện:
2x\(^2\) + 10y\(^2\) – 6xy – 6x – 2y + 10 = 0
Hãy tính giá trị của biểu thức: A = [(x + y – 4)2018 – y2018] : x
\(2x^2+10y^2-6xy-6x-2y+10=0\)
\(\Leftrightarrow x^2-6xy+9y^2+x^2-6x+9+y^2-2y+1=0\)
\(\Leftrightarrow\left(x-3y\right)^2+\left(x-3\right)^2+\left(y-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3y=0\\x-3=0\\y-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
Vậy \(A=\dfrac{\left(x+y-4\right)^{2018}-y^{2018}}{x}=\dfrac{0^{2018}-1^{2018}}{3}=-\dfrac{1}{3}\)
Đúng 4
Bình luận (0)
Cho hàm số
y
f
(
x
)
log
3
(
e
x
2
-
x
2018
)...
Đọc tiếp
Cho hàm số y = f ( x ) = log 3 ( e x 2 - x 2018 ) .Khi đó f’(1) bằng
![]()
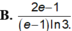
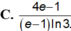
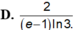
Cho \(0\le x,y\le\dfrac{1}{2}\).CM: \(\dfrac{\sqrt{x}}{1+y}+\dfrac{\sqrt{y}}{1+x}\le\dfrac{2\sqrt{2}}{3}\)
Cho hàm số y f(x) có đồ thị của hàm số yf(x) như hình vẽ bên. Biết f(-2)0. Hàm số
y
f
1
-
x
2018
đồng biến trên khoảng nào dưới đây? A.
-
3
2018
;...
Đọc tiếp
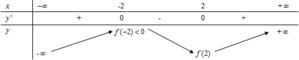
Cho hàm số y = f(x) có đồ thị của hàm số y=f'(x) như hình vẽ bên. Biết f(-2)<0. Hàm số y = f 1 - x 2018 đồng biến trên khoảng nào dưới đây?
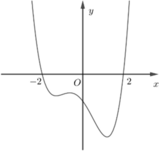
A. - 3 2018 ; 3 2018
B. - 1 ; + ∞
C. - ∞ ; - 3 2018
D. - 3 2018 ; 0
Cho 2 số thực x,y thoả mãn x2 + y2 ≤ x + y . CHứng minh rằng x + y ≤ 2
Do \(x^2+y^2\ge0\) \(\forall x;y\Rightarrow x+y\ge0\)
Lại có \(x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\Rightarrow x+y\ge\frac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x+y\right)-\left(x+y\right)^2\ge0\Rightarrow\left(x+y\right)\left(2-\left(x+y\right)\right)\ge0\)
- Nếu \(x+y=0\Rightarrow x+y< 2\) BĐT đúng
- Nếu \(x+y>0\Rightarrow2-\left(x+y\right)\ge0\Rightarrow x+y\le2\)
Vậy \(x+y\le2\)
Đúng 0
Bình luận (0)