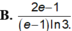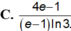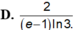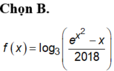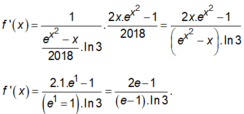Các câu hỏi tương tự
Cho hàm số
y
f
(
x
)
có
f
(
2
)
2
,
f
(
3
)
5
hàm số
y
f
(
x
)
liên tục trên [2;3]. Khi đó
∫
2
3
f
(
x
)
d
x
bằng:
Đọc tiếp
Cho hàm số y = f ( x ) có f ( 2 ) = 2 , f ( 3 ) = 5 hàm số y = f ' ( x ) liên tục trên [2;3]. Khi đó ∫ 2 3 f ' ( x ) d x bằng:
![]()
![]()
![]()
![]()
Cho y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x - 3 ) 2 . Khi đó số cực trị của hàm số y = f ( 2 x + 1 ) là
A. 0
B. 2
C. 1
D. 3
Cho hàm số y f(x) có
f
(
x
)
1
x
+
1
. Biết rằng f(0) 2018. Giá trị của biểu thức f(3)-f(1) bằng: A. ln2 B. ln4 C. ln3 D. 2ln2
Đọc tiếp
Cho hàm số y = f(x) có f ' ( x ) = 1 x + 1 . Biết rằng f(0)= 2018. Giá trị của biểu thức f(3)-f(1) bằng:
A. ln2
B. ln4
C. ln3
D. 2ln2
Biết nguyên hàm của hàm số y = f(x) là F ( x ) = x 2 + 4 x + 1 . Khi đó f(3) bằng:
A. 6
B. 10
C. 22
D. 30
Cho hàm số y f( x) ax4+ bx3+ cx2+ dx+ e với a ≠0. Biết rằng hàm số y f( x) có đạo hàm là f’(x) và hàm số y f’(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai? A. Trên khoảng (-2; 1) thì hàm số y f( x) luôn tăng. B. Hàm số y f(x) giảm trên đoạn [ -1; 1] . C. Hàm số y f( x) đồng biến trên khoảng (1+ ∞) . D. Hàm số y f( x) nghịch biến trên khoảng (- ∞; -2)
Đọc tiếp
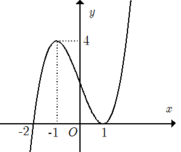
Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e với a ≠0. Biết rằng hàm số y= f( x) có đạo hàm là f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?
A. Trên khoảng (-2; 1) thì hàm số y= f( x) luôn tăng.
B. Hàm số y= f(x) giảm trên đoạn [ -1; 1] .
C. Hàm số y= f( x) đồng biến trên khoảng (1+ ∞) .
D. Hàm số y= f( x) nghịch biến trên khoảng (- ∞; -2)
Cho hàm số f(x)= x(x-1)(x-2) (x-3)... (x-2018).
Tính f'(1)
A. -2017!
B. 0
C. 2017!
D. 2018
Biết nguyên hàm của hàm số y=f(x) là F x = x 2 + 4 x + 1 . Khi đó f(3) bằng
A. 6
B. 10
C. 22
D. 30
Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(0) – F(1) bằng
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(0) – F(1) bằng
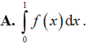
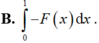

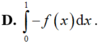
Cho hàm số y=f(x) có đạo hàm liên tục trên (1;+\(\infty\)); f(x)>0,\(\forall\)x\(\in\)(1;+\(\infty\)), f(2)=1 và thỏa mãn f(x)=x[2(f(x))\(^2\)+f'(x)] khi đó tích phân từ 2 đến 3 của f(x) bằng ?
GIÚP MÌNH VỚI