Rút gọn
B=-1+1/2-1/2^2+...-1/2^2n+1/2^2n+1

Những câu hỏi liên quan
Rút gọn:
B= \(\frac{1^2}{2^2-1}.\frac{3^2}{4^2-1}.\frac{5^2}{6^2-1}....\frac{\left(2n+1\right)^2}{\left(2n+2\right)^2-1}\)
\(B=\frac{1^2}{2^2-1}.\frac{3^2}{4^2-1}.\frac{5^2}{6^2-1}...\frac{\left(2n+1\right)^2}{\left(2n+2\right)^2-1}\)
\(=\frac{1^2}{\left(2-1\right)\left(2+1\right)}.\frac{3^2}{\left(4-1\right)\left(4+1\right)}...\frac{\left(2n+1\right)^2}{\left(2n+2-1\right)\left(2n+2+1\right)}\)
\(=\frac{1}{1.3}.\frac{3^2}{3.5}...\frac{\left(2n+1\right)^2}{\left(2n+1\right)\left(2n+3\right)}\)
\(=\frac{1}{2n+3}\)
Đúng 0
Bình luận (0)
Rút gọn :\(A=\frac{1}{1.3}+\frac{1}{2.4}+\frac{1}{3.5}+\frac{1}{4.6}+...+\frac{1}{\left(2n-1\right)\left(2n+1\right)}+\frac{1}{2n\left(2n+2\right)}\)
tự làm là hạnh phúc của mỗi công dân.
1. Chứng minh : B left(1-frac{2}{6}right).left(1-frac{2}{12}right).left(1-frac{2}{20}right)...left(1-frac{2}{nleft(n+1right)}right)frac{1}{3}2. cho M frac{1}{1.left(2n-1right)}+frac{1}{3.left(2n-3right)}+frac{1}{5.left(2n-5right)}+...+frac{1}{left(2n-3right).3}+frac{1}{left(2n-1right).1}N 1+frac{1}{3}+frac{1}{5}+...+frac{1}{2n-1}Rút gọn frac{M}{N}
Đọc tiếp
1. Chứng minh : B = \(\left(1-\frac{2}{6}\right).\left(1-\frac{2}{12}\right).\left(1-\frac{2}{20}\right)...\left(1-\frac{2}{n\left(n+1\right)}\right)>\frac{1}{3}\)
2. cho M = \(\frac{1}{1.\left(2n-1\right)}+\frac{1}{3.\left(2n-3\right)}+\frac{1}{5.\left(2n-5\right)}+...+\frac{1}{\left(2n-3\right).3}+\frac{1}{\left(2n-1\right).1}\)
N = \(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{2n-1}\)
Rút gọn \(\frac{M}{N}\)
Rút gọn biểu thức
A
3
1
.
2
+
5
(
2
.
3
)
2
+
.
.
.
+
2
n
+
1
[
n
(
n
+
1
)...
Đọc tiếp
Rút gọn biểu thức A = 3 1 . 2 + 5 ( 2 . 3 ) 2 + . . . + 2 n + 1 [ n ( n + 1 ) ] 2
Xét biểu thức tổng quát: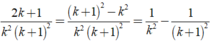
Khi đó ta có: 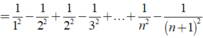
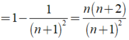
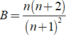
Vậy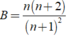
Đúng 0
Bình luận (0)
(1^2/1.3)+(2^2/3.5)+....+(n^2/(2n-1)(2n+1))=(n(n+1))/((2n-1)(2n+1))
Đặt A = 1/1.3 + 1/3.5 + 1/5.7 +........+ 1/(2n - 1)(2n + 1)
2.A = 2/1.3 + 2/3.5 + 2/5.7 +........+ 2/(2n - 1)(2n + 1)
2.A = 1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 + ..... + 1/(2n - 1) - 1/(2n + 1)
2.A = 1 - 1/(2n + 1) = 2n/(2n + 1)
Vậy A = n/(2n + 1)
Đúng 0
Bình luận (0)
cho1/2cănx-1/2cănx+2-cănx/1-x
a,tìm đk và rút gọn
b,x=4/9
Đề có phải là \(\dfrac{1}{2\sqrt{x}}-\dfrac{1}{2\sqrt{x}}+\dfrac{2-\sqrt{x}}{1-x}\) không bạn?
Đúng 0
Bình luận (1)
Tìm số nguyên dương n sao cho \(C_{2n+1}^1-2.2.C_{2n+1}^2+3.2^2.C_{2n+1}^3-...+\left(2n+1\right).2^{2n}.C_{2n+1}^{2n+1}=2019\)
Xét khai triển:
\(\left(1+2x\right)^{2n+1}=C_{2n+1}^0+C_{2n+1}^1.2x+C_{2n+1}^2\left(2x\right)^2+...+C_{2n+1}^{2n+1}\left(2x\right)^{2n+1}\)
Đạo hàm 2 vế:
\(2\left(2n+1\right)\left(1+2x\right)^{2n}=2C_{2n+1}^1+2^2C_{2n+1}^2x+...+\left(2n+1\right)2^{2n+1}C_{2n+1}^{2n+1}x^{2n}\)
\(\Leftrightarrow\left(2n+1\right)\left(1+2x\right)^{2n}=C_{2n+1}^1+2C_{2n+1}^2x+...+\left(2n+1\right)2^{2n}C_{2n+1}^{2n+1}x^{2n}\)
Cho \(x=-1\) ta được:
\(2n+1=C_{2n+1}^1-2C_{2n+1}^2+...+\left(2n+1\right)2^{2n}C_{2n+1}^{2n+1}\)
\(\Rightarrow2n+1=2019\Rightarrow n=1009\)
Đúng 2
Bình luận (0)
M=\(\left(\dfrac{x}{x-2}-\dfrac{x+1}{x+2}-\dfrac{2x+7}{x^{2^{ }}-4}\right):\left(\dfrac{3-x}{x-2}+1\right)\)
a,rút gọn
b,tìm x để M <1
a. ĐK: \(x\ne\pm2\)
\(M=\left[\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2x+7}{\left(x-2\right)\left(x+2\right)}\right]:\dfrac{3-x+x-2}{x-2}\)
\(=\dfrac{x^2+2x-\left(x^2-2x+x-2\right)-2x-7}{\left(x-2\right)\left(x+2\right)}.\left(x-2\right)\)
\(=\dfrac{x-5}{x+2}\)
b. \(\dfrac{x-5}{x+2}< 1\Leftrightarrow\dfrac{x-5}{x+2}-1< 0\)
\(\Leftrightarrow\dfrac{-7}{x+2}< 0\Leftrightarrow x+2>0\)
\(\Leftrightarrow x>-2\)
Vậy \(x>-2,x\ne2\)
Đúng 2
Bình luận (0)
Rút gọn biểu thức sau A=(3/1.2)^2+(5/2.3)^2+(7/3.4)^2+...+(2n+1/n^2+1)^2




















