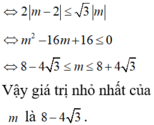CMR: Không tồn tại \(x,y,z\in\)N* , sao cho \(x^3+y^3=z^3\)

Những câu hỏi liên quan
CMR: Không tồn tại x,y,z \(\in\)N* sao cho \(x^3+y^3=z^3\)
P/s: Hóng nhân tài
Chứng minh rằng không tồn tại ba số hữu tỉ x, y, z sao cho: \(xy=\frac{13}{15}\); \(yz=\frac{1}{3}\); \(zx=\frac{-3}{13}\)
Chứng minh rằng không tồn tại x thuộc Z sao cho x2+2012x-20112011-1=0
Ta có : \(x^2+2012x+2011^{2011}-1=0\)
\(\Leftrightarrow x^2+2012x+1006^2=2011^{2011}+1+1006^2\)
\(\Rightarrow\left(x+1006\right)^2=2011^{2011}+1+1006^2\)
Giả sử x là một số nguyên thì VT là một số chính phương.
Khi đó VP cũng là số chính phương.
Lại có 20112011 có tận cùng là chữ số 1, 10062 có tận cùng là chữ số 6 nên VP có tận cùng là chữ số 8.
Lại có không một số chính phương nào có tận cùng là chữ số 8 hay VP không là số chính phương.
Vậy giả sử sai hay không tồn tại số nguyên x thỏa mãn phương trình trên.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
m
)
:
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S m ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - m ) 2 = m 2 4 và hai điểm A(2;3;5), B(1;2;4). Tìm giá trị nhỏ nhất của m để trên ( S m ) tồn tại điểm M sao cho M A 2 - M B 2 = 9 .
A. m=1
B. m= 3 - 3
C. m= 8 - 4 3
D. m= 4 - 3 2
Cho x,y,z là các số nguyên dương sao cho x+y+z=3
CMR : P = \(\dfrac{1}{x^2+x}+\dfrac{1}{y^2+y}+\dfrac{1}{z^2+z}\ge\dfrac{3}{2}\)
+,3 = x + y + z \(\ge\) \(3\sqrt[3]{xyz}\Rightarrow xyz\le1\)
+, P \(\ge\) \(3\sqrt[3]{\dfrac{1}{xyz\left(x+1\right)\left(y+1\right)\left(z+1\right)}}\ge\dfrac{3}{\sqrt[3]{\left(x+1\right)\left(y+1\right)\left(z+1\right)}}\ge\dfrac{3}{\dfrac{x+y+z+3}{3}}=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
CMR \(x^3+y^3+z^3-x-y-z⋮6\forall x,y,z\in Z\)
Lời giải:
\(A=x^3+y^3+z^3-x-y-z\)
\(A=\left(x^3-x\right)+\left(y^3-y\right)+\left(z^3-z\right)\)
\(A=x\left(x^2-1\right)+y\left(y^2-1\right)+z\left(z^2-1\right)\)
\(A=x\left(x-1\right)\left(x+1\right)+y\left(y-1\right)\left(y+1\right)+z\left(z-1\right)\left(z+1\right)\)
\(A=\left(x-1\right)x\left(x+1\right)+\left(y-1\right)y\left(y+1\right)+\left(z-1\right)z\left(z+1\right)\)
Ta có:\(\left\{{}\begin{matrix}x-1;x;x+1\\y-1;y;y+1\\z-1;z;z+1\end{matrix}\right.\) là 3 số tự nhiên liên tiếp
Suy ra: \(\left\{{}\begin{matrix}\left(x-1\right)x\left(x+1\right)\\\left(y-1\right)y\left(y+1\right)\\\left(z-1\right)z\left(z+1\right)\end{matrix}\right.\) chia hết cho \(6\)
Hay \(A⋮6\left(đpcm\right)\)
Đúng 0
Bình luận (0)
cho 3 số thực x,y,z sao cho x+y+z=1 CMR
\(x^3+y^3+z^3-3xyz=\frac{1}{2}\left(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right)\)
VT=\(x^3+y^3+z^3-3xyz=\left(x+y\right)^3+z^3-3x^2y-3xy^2-3xyz\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy.\left(x+y+z\right)\)
\(=\left(x+y\right)^2-\left(x+y\right).z+z^2-3xy\left(\text{vì }x+y+z=1\right)\)
\(=x^2+2xy+y^2-xz-yz+z^3-3xy\)
\(=x^2+y^2+z^2-xy-yz-xz\)
\(=\frac{1}{2}.\left(2x^2+2y^2+2z^2-2xy-2yz-2xz\right)\)
\(=\frac{1}{2}.\left[\left(x^2-2xy-y^2\right)+\left(y^2-2yz+z^2\right)+\left(x^2-2xz+z^2\right)\right]\)
\(=\frac{1}{2}.\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\)=VP
=>dpcm
Đúng 0
Bình luận (0)
Ta có : \(x^3+y^3+z^3-3xyz=\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3xyz\)
\(=x+y+z\left(x^2+y^2+z^2+2xy+xz+yz\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
\(=x^2+y^2+z^2-xy-yz-xz=\frac{\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2xz+x^2\right)}{2}=\frac{1}{2}\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\)
Đúng 0
Bình luận (0)
Cho 3 số thực x,y,z đôi một phân biệt sao cho
\(\left(y-z\right)\sqrt[3]{1-x^3}+\left(z-x\right)\sqrt[3]{1-y^3}+\left(x-y\right)\sqrt[3]{1-z^3}=0\)
CMR: \(\left(1-x^3\right)\left(1-y^3\right)\left(1-z^3\right)=\left(1-xyz\right)^3\)
CHO X,Y,Z LÀ CÁC SỐ THỰC KHÔNG ÂM THỎA MÃN X+Y+Z=3 VÀ XY+YZ+ZX KHÁC 0 . CMR :
\(\frac{x+1}{y+1}+\frac{y+1}{z+1}+\frac{z+1}{x+1}\le\frac{25}{3\sqrt[3]{4.\left(xy+yz+zx\right)}}\)
thanks in advance <3
Áp dụng BĐT AM-GM: $VP\leq \frac{25}{yz+zx+xy+4}$
Cần c/m: $\frac{x+1}{y+1}+\frac{y+1}{z+1}+\frac{z+1}{x+1}$\leq \frac{25}{yz+zx+xy+4}$
$\Leftrightarrow (yz+zx+xy)(xy^{2}+yz^{2}+zx^{2})+4(xy^{2}+yz^{2}+zx^{2})\leq 25xyz+4(yz+zx+xy)+16$
BĐT trên sẽ được c/m nếu c/m được: $xy^{2}+yz^{2}+zx^{2}\leq 4$.
KMTTQ, g/sử y nằm giữa x và z. $\Rightarrow x(x-y)(y-z)\geq 0$
$\Leftrightarrow xy^{2}+yz^{2}+zx^{2}\leq y(x^{2}+xz+z^{2})\leq y(x+z)^{2}$
Đến đây áp dụng BĐT AM-GM:
$y(x+z)^{2}=4.y.(\frac{x+z}{2})(\frac{x+z}{2})\leq \frac{4(y+\frac{x+z}{2}+\frac{x+z}{2})^{3}}{27}=\frac{4(x+y+z)^{3}}{27}=4$ (đpcm)
Dấu bằng xảy ra khi, chẳng hạn $x=0;y=1;z=2$
Áp dụng BĐT AM-GM và BĐT Rearrangement ta có:
\(VT=\frac{x+1}{y+1}+\frac{y+1}{z+1}+\frac{z+1}{x+1}\)
\(=\frac{\left(x+y+z\right)^2+3\left(x+y+z\right)+xy^2+yz^2+zx^2+3}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)\(\le\frac{21+y\left(x+z\right)^2}{3\sqrt[3]{4\left(xy+yz+xz\right)}}\le\frac{21+\frac{\left(\frac{2\left(x+y+z\right)}{3}\right)^3}{2}}{3\sqrt[3]{4\left(xy+yz+zx\right)}}=\frac{21+4}{3\sqrt[3]{4\left(xy+yz+zx\right)}}=\frac{25}{3\sqrt[3]{4\left(xy+yz+zx\right)}}\)
Dấu "=" xảy ra <=> (x;y;z)=(2;1;0) và hoán vị của nó
xml hkjmf,gkjbhvn jbkvmcbnvdyjxnbv hjgfvchjwbfhyergfvyug h ghbf vchdsvhdc ghv eucbtrgvtcfrtfvgtcb tybk cjvh dgsx hjutygfvhyfhefrd cr fb kosciugyrturikjht54tr273r6734vn cjhvdfbv dfjbgerutjh37347t567 t gn fvbrhkjbfghty 66u 67gfbrhtb vbnbdffrhg ';\ hvgn hvbhzxn cb gvfycbher 74y6t5rbfvnhsgt hbgvdhcvhjgey6t5u gewytdfjbxjhdv bn 6t5675t47t5648b gryjhvdhybgfvdghv d vdfstrcdgvcc ghfvdshvh bbv3rt364tr bgryjhvbnh vznhbbcv nbmhfbvdghbv mhdfbdschmaewugugf ygvrfyug s g dg vyga4ut53746r87hyu rf5ygygcsrbv sdbv x vc bgyergty4gfytrfygtyfgrgyfyjugrfauygfugdv euygt674y4375y74
Xem thêm câu trả lời