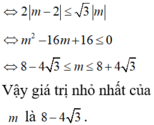Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;-2;2) và mật cầu (S):
x
2
+
y
2
+
(
z
-
1
)
2
4
. Điểm M di chuyển trên mặt cầu (S) đồng thời thỏa mãn
O...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;-2;2) và mật cầu (S): x 2 + y 2 + ( z - 1 ) 2 = 4 . Điểm M di chuyển trên mặt cầu (S) đồng thời thỏa mãn O M → . A M → = 6 . Điểm M luôn thuộc mặt phẳng nào dưới đây?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm
A
(
2
;
3
;
2
)
,
B
(
-
2
;
-
1
;
4
)
. Tìm tọa độ điểm E thuộc trục Oz sao cho E cách đều hai điểm A, B
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A ( 2 ; 3 ; 2 ) , B ( - 2 ; - 1 ; 4 ) . Tìm tọa độ điểm E thuộc trục Oz sao cho E cách đều hai điểm A, B
![]()
![]()
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) (x-6)
x
2
+
4
trên đoạn [0;3] có dạng a - b
c
với a là số nguyên và b, c là các số nguyên dương. Tính S a + b + c. A. 4 B. -2 C. -22 D. 5
Đọc tiếp
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
A. 4
B. -2
C. -22
D. 5
Cho
z
x
+
y
i
với x, y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2
-
3
i
≤
|
z
+
i
-
2
|
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ...
Đọc tiếp
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
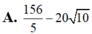
![]()
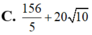
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng (P): 2x + y - 4z + 1 0. Đường thẳng (d) đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d. A.
x
1
+
5
t
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng (P): 2x + y - 4z + 1 =0. Đường thẳng (d) đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
A. x = 1 + 5 t y = 2 - 6 t z = 3 + t
B. x = t y = 2 t z = 2 + t
C. x = 1 + 3 t y = 2 + 2 t z = 3 + t
D. x = 1 - t y = 2 + 6 t z = 3 + t
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác cân tại A và
B
A
C
^
120
∘
,
B
C
2a. Gọi M, N lần lượt là hình chiếu của điểm A trên SB, SC. Tính bán kính mặt cầu đi qua bốn điểm A, N, M, B.
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác cân tại A và B A C ^ = 120 ∘ , B C = 2a. Gọi M, N lần lượt là hình chiếu của điểm A trên SB, SC. Tính bán kính mặt cầu đi qua bốn điểm A, N, M, B.
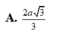
![]()
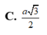
![]()
Trong không gian Oxyz, cho tam giác ABC với A(1;2;5), B(3;4;1), C(2;3;-3). Gọi G là trọng tâm tam giác ABC và M là điểm thay đổi trên (Oxz). Độ dài GM ngắn nhất bằng A. 2 B. 3 C. 4 D. 1
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC với A(1;2;5), B(3;4;1), C(2;3;-3). Gọi G là trọng tâm tam giác ABC và M là điểm thay đổi trên (Oxz). Độ dài GM ngắn nhất bằng
A. 2
B. 3
C. 4
D. 1
Trong không gian Oxyz, cho tam giác ABC với
A
(
1
;
2
;
5
)
,
B
(
3
;
4
;
1
)
,
C
(
2
;
3
;
-
3
)
. Gọi G là trọng tâm tam giác ABC và M là điểm thay đổi trên mp(Oxz). Độ dài GM ngắn nhất bằng A. 2 B. 3 C. 4 D. 1
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC với A ( 1 ; 2 ; 5 ) , B ( 3 ; 4 ; 1 ) , C ( 2 ; 3 ; - 3 ) . Gọi G là trọng tâm tam giác ABC và M là điểm thay đổi trên mp(Oxz). Độ dài GM ngắn nhất bằng
A. 2
B. 3
C. 4
D. 1
Trong không gian Oxyz cho hai mặt phẳng (P): x-y+2z-30, (Q): x-y+2z+30 có bao nhiêu điểm M có hoành độ nguyên thuộc Ox sao cho tổng khoảng cách từ M đến hai mặt phẳng (P), (Q) bằng khoảng cách giữa (P) và (Q). A. 2 B. 4 C. 6 D. 7
Đọc tiếp
Trong không gian Oxyz cho hai mặt phẳng (P): x-y+2z-3=0, (Q): x-y+2z+3=0 có bao nhiêu điểm M có hoành độ nguyên thuộc Ox sao cho tổng khoảng cách từ M đến hai mặt phẳng (P), (Q) bằng khoảng cách giữa (P) và (Q).
A. 2
B. 4
C. 6
D. 7