Giải phương trình sau
\(\dfrac{cos3x-cosx}{1+sinx}=0\)
Những câu hỏi liên quan
Giải phương trình: \(sin3x-cos3x+sinx+cosx=\dfrac{1}{sin3x+cosx}-\dfrac{1}{cos3x-sinx}\)
ĐKXĐ: ...
\(sin3x-cos3x+sinx+cosx=\dfrac{sin3x-cos3x+sinx+cosx}{\left(sin3x+cosx\right)\left(cos3x-sinx\right)}\)
\(\Rightarrow\left[{}\begin{matrix}sin3x-cos3x+sinx+cosx=0\left(1\right)\\\left(sin3x+cosx\right)\left(cos3x-sinx\right)=1\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow3sinx-4sin^3x-4cos^3x+3cosx+sinx+cosx=0\)
\(\Leftrightarrow sinx+cosx+sin^3x+cos^3x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)\left(1-sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2-sinx.cosx\right)=0\)
\(\Leftrightarrow sinx+cosx=0\) (loại)
(2) \(\Leftrightarrow sin3x.cos3x-sinx.cosx-sin3x.sinx+cos3x.cosx=1\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x+cos4x=1\)
\(\Leftrightarrow\dfrac{1}{2}\left(3sin2x-4sin^32x\right)-\dfrac{1}{2}sin2x+1-2sin^22x=1\)
\(\Leftrightarrow sin2x-2sin^32x-2sin^22x=0\)
\(\Leftrightarrow-sin2x\left(2sin^22x+2sin2x-1\right)=0\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Giải phương trình sin3x(cosx - 2sin3x) + cos3x(1 + sinx - 2cos3x) 0 A. x ±
π
3
+ k2π, k ∈ Z B. x
π
4
+ kπ, k ∈ Z C. x
-
π
4
+ k2π, x
-
π
6
+ k2π,k ∈ Z D. Vô nghiệm
Đọc tiếp
Giải phương trình sin3x(cosx - 2sin3x) + cos3x(1 + sinx - 2cos3x) = 0
A. x = ± π 3 + k2π, k ∈ Z
B. x = π 4 + kπ, k ∈ Z
C. x = - π 4 + k2π, x = - π 6 + k2π,k ∈ Z
D. Vô nghiệm
Giải phương trình:
1,\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
2,\(|cosx-sinx|+2sin2x=1\)
3,\(2sin2x-3\sqrt{6}|sinx+cosx|+8=0\)
4,\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
3.
\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)
\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)
...
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình cosx+cos3x=sinx-sin3x
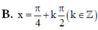
Giải phương trình lượng giác bậc nhất đối với sinx và cosx:
\(cos3x-sinx=\sqrt{3}\left(cosx-sin3x\right)\)
\(\Leftrightarrow cos3x+\sqrt{3}sin3x=\sqrt{3}cosx+sinx\)
\(\Leftrightarrow\dfrac{1}{2}cos3x+\dfrac{\sqrt{3}}{2}sin3x=\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx\)
\(\Leftrightarrow cos\left(3x-\dfrac{\pi}{3}\right)=cos\left(x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{3}=x-\dfrac{\pi}{6}+k2\pi\\3x-\dfrac{\pi}{3}=\dfrac{\pi}{6}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình sinx + sin2x + sin3x= cosx + cos2x+ cos3x
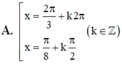
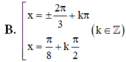
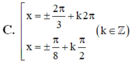
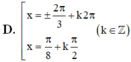
Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
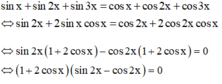
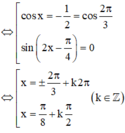
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm
Đúng 0
Bình luận (0)
giải phương trình lượng giác
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
ĐK: \(x\ne\dfrac{\pi}{6}+k2\pi;x\ne\dfrac{5\pi}{6}+k2\pi\)
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=0\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=0\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đối chiếu điều kiện ta được \(x=-\dfrac{5\pi}{6}+k2\pi\).
Đúng 0
Bình luận (0)
III. Phương trình bậc nhất đối với sinx và cosx:*Giải các phương trình bậc nhất đối với sinx và cosx sau đây:(2.1)1) 2sinx-2cosxsqrt{2}2) cosx-sqrt{3}sinx13) sqrt{3}sindfrac{x}{3}+cosdfrac{x}{2}sqrt{2}4) cosx-sinx15) 2cosx+2sinxsqrt{6}6) sin3x+sqrt{3}cosxsqrt{2}7) 3sinx-2cosx2(2.3)1) left(sinx-1right)left(1+cosxright)cos^2x2) sinleft(dfrac{pi}{2}+2xright)+sqrt{3}sinleft(pi-2xright)13) sqrt{2}left(cos^4x-sin^4xright)cosx+sinx4) sin2x+cos2xsqrt{2}sin3x5) sinxsqrt{2}sin5x-cosx6) sin8x-cos6xsqrt{3}l...
Đọc tiếp
III. Phương trình bậc nhất đối với sinx và cosx:
*Giải các phương trình bậc nhất đối với sinx và cosx sau đây:
(2.1)
1) \(2sinx-2cosx=\sqrt{2}\)
2) \(cosx-\sqrt{3}sinx=1\)
3) \(\sqrt{3}sin\dfrac{x}{3}+cos\dfrac{x}{2}=\sqrt{2}\)
4) \(cosx-sinx=1\)
5) \(2cosx+2sinx=\sqrt{6}\)
6) \(sin3x+\sqrt{3}cosx=\sqrt{2}\)
7) \(3sinx-2cosx=2\)
(2.3)
1) \(\left(sinx-1\right)\left(1+cosx\right)=cos^2x\)
2) \(sin\left(\dfrac{\pi}{2}+2x\right)+\sqrt{3}sin\left(\pi-2x\right)=1\)
3) \(\sqrt{2}\left(cos^4x-sin^4x\right)=cosx+sinx\)
4) \(sin2x+cos2x=\sqrt{2}sin3x\)
5) \(sinx=\sqrt{2}sin5x-cosx\)
6) \(sin8x-cos6x=\sqrt{3}\left(sin6x+cos8x\right)\)
7) \(cos3x-sinx=\sqrt{3}\left(cosx-sin3x\right)\)
8) \(2sin^2x+\sqrt{3}sin2x=3\)
9) \(sin^4x+cos^4\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{4}\)
(2.3)
1) \(\dfrac{\sqrt{3}\left(1-cos2x\right)}{2sinx}=cosx\)
2) \(cotx-tanx=\dfrac{cosx-sinx}{sinx.cosx}\)
3) \(\dfrac{\sqrt{3}}{cosx}+\dfrac{1}{sinx}=4\)
4) \(\dfrac{1+sinx}{1+cosx}=\dfrac{1}{2}\)
5) \(3cosx+4sinx+\dfrac{6}{3cosx+4sinx+1}=6\)
(2.4)
a) Tìm nghiệm \(x\in\left(\dfrac{2\pi}{5};\dfrac{6\pi}{7}\right)\) của phương trình \(cos7x-\sqrt{3}sin7x+\sqrt{2}=0\)
b) Tìm nghiệm \(x\in\left(0;\pi\right)\) của phương trình \(4sin^2\dfrac{x}{2}-\sqrt{3}cos2x=1+2cos^2\left(x-\dfrac{3\pi}{4}\right)\)
(2.5) Xác định tham số m để các phương trình sau đây có nghiệm:
a) \(mcosx-\left(m+1\right)sinx=m\)
b) \(\left(2m-1\right)sinx+\left(m-1\right)cosx=m-3\)
(2.6) Tìm GTLN, GTNN (nếu có) của các hàm số sau đây:
a) \(y=3sinx-4cosx+5\)
b) \(y=cos2x+sin2x-1\)
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c.
\(\sqrt{3}sin\dfrac{x}{3}+cos\dfrac{x}{2}=\sqrt{2}\)
Câu này đề đúng không nhỉ? Nhìn thấy có vẻ không đúng lắm
d.
\(cosx-sinx=1\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Giải các phương trình sau:
1+cosx+cos2x+cos3x=0
sinx+sin3x+sin5x=cosx+cos3x+cos5x
MỌI NGƯỜI GIÚP MÌNH VỚI MÌNH CẢM ƠN
giải phương trình sau:
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}\)=0
ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)
\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)
\(\Leftrightarrow2cos^22x-2cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)
Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)