Chứng minh bất đẳng thức
3b² +a²+2ab+2a+6b+3>=0
Những câu hỏi liên quan
CHứng minh : A=n^2-2ab=2a+11b^2+6b+2016
Chứng minh rằng với mọi số a,b,c ta luôn có :
a) a2 + 5b2 - 4ab + 2a - 6b + 3 > 0
b) a2 + 2b - 2ab + 2a - 4b + 2 >0
23 tháng 4 2020 lúc 11:06
Chứng minh các bất đẳng thức sau bằng cách biến đổi tương đương:
a) Cho 1\(\le t\le\) 2. CMR: \(\frac{t^2}{2.t^2+3}+\frac{2}{1+t}\ge\frac{34}{33}\)
b) Chứng minh với mọi số duong a, b ta luôn có \(\frac{a^2b}{2a^3+b^3}+\frac{2}{3}\ge\frac{a^2+2ab}{2a^2+b^2}\)
Định đi ngủ mà chợt nhớ lúc chiều có hứa là làm giúp chủ tus nên h phải làm =)))
Đúng 0
Bình luận (0)
chứng minh bất đẳng thức 2a^3+8a<=a^4+16
\(2a^3+8a\le a^4+16\)
\(\Leftrightarrow2a^3+8a-a^4-16\le0\)
\(\Leftrightarrow\left(2a^3-a^4\right)+\left(8a-16\right)\le0\)
\(\Leftrightarrow-a^3\left(a-2\right)+8\left(a-2\right)\le0\)
\(\Leftrightarrow-\left(a-2\right)\left(a^3-8\right)\le0\Leftrightarrow-\left(a-2\right)^2\left(a^2+2a+4\right)\le0\)
TA THẤY : \(\left(a-2\right)^2\left(a^2+2a+4\right)\ge0\)\(\Leftrightarrow-\left(a-2\right)^2\left(a^2+2a+4\right)\le0\)\(\Leftrightarrow2a^3+8a\le a^4+16\left(dpcm\right)\)
DẤU " = " XẢY RA KHI X = 2
TK CHO MK NKA !!!
Đúng 0
Bình luận (0)
chứng minh đẳng thức: - (a - 3b - c) - (2a + b + c) = (5a - 4b +2c) - (8a - 6b +2c)
Chứng minh bất đẳng thức a, 2a-3>2b-3( với a>b. b, -3a+5> -3b+2 ( với a
a) a > b
⇒ 2a > 2b (nhân hai vế với 2 > 0)
⇒ 2a - 3 > 2b - 3 (cộng hai vế với -3)
b) a < b
⇒ -3a > -3b (nhân hai vế với -3 < 0)
⇒ -3a + 2 > -3b + 2 (1) (cộng hai vế với 2)
5 > 2
⇒ -3a + 5 > -3a + 2 (2) (cộng hai vế với -3a)
Từ (1) và (2) ⇒ -3a + 5 > -3b + 2
Đúng 0
Bình luận (0)
Chứng minh bất đẳng thức a^2+b^2 >= 2ab
Giải
(a^2+b^2)-2ab=(a-b)^2 >=0
Vế \(\left(a-b\right)^2\ge0\)là sao mà có vậy
Ta dùng hằng đẳng thức
(a^2 + b^2) - 2ab = a^2 - 2ab + b^2 = (a-b)^2.
Mà (a-b)^2 >= 0 nên ta suy ra a^2+b^2 >= 2ab.
Nhơ k nha
Đúng 100% đó
Đúng 0
Bình luận (0)
Bài này mà là toán lớp 3 á ??????????
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 3 số thực a, b, c thỏa mãn a + b + c ≤ 1. Chứng minh bất đẳng thức: 1/(a^2 + 2bc) + 1/(b^2 + 2ca) + 1/(c^2 + 2ab) ≥ 9
3 số thực dương nhé.
Áp dụng bất đẳng thức Cauchy Schwarz dạng Engel có :
\(\frac{1}{a^2+2bc}+\frac{1}{b^2+2ca}+\frac{1}{c^2+2ab}\ge\frac{\left(1+1+1\right)^2}{\left(a^2+2bc\right)+\left(b^2+2ca\right)+\left(c^2+2ab\right)}=\frac{9}{\left(a+b+c\right)^2}\ge\frac{9}{1^2}=9\)
Dấu bằng xảy ra \(\Leftrightarrow\frac{1}{a^2+2bc}=\frac{1}{b^2+2ca}=\frac{1}{c^2+2ab}\)và \(a+b+c=1\)
\(\Leftrightarrow a^2+2bc=b^2+2ca=c^2+2ab\)
Mong có ai giúp mình từ đẳng thức trên giải ra a=b=c.
Đúng 0
Bình luận (0)
a=b=c ket hop voi a+b+c=<1 =>a=b=c=1/3 nhe
Đúng 0
Bình luận (0)
\(a^2+2bc=b^2+2ca=c^2+2ab\)
Ta có: \(\hept{\begin{cases}a^2+2bc=b^2+2ca\\b^2+2ca=c^2+2ab\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(a-b\right)\left(a+b\right)-2c\left(a-b\right)=0\\\left(b-c\right)\left(b+c\right)-2a\left(b-c\right)=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(a-b\right)\left(a+b-2c\right)=0\\\left(b-c\right)\left(b+c-2a\right)=0\end{cases}}\)
Tới đây thì suy được ra là \(a=b=c\) rồi nhé Trần Thùy Dung - Trang của Trần Thùy Dung - Học toán với OnlineMath
Đúng 0
Bình luận (0)
a) Cho a>b>0 thỏa mãn a3+b3 = a-b. Chứng minh a2 + ab + b2 < 1
b) Chứng minh bất đẳng thức sau: a2 + 2b2 + 2c2 >= 2ab - 2ac + bc
Chứng minh các đẳng thức sau:
a
+
b
b
2
a
2
b
4
a
2
+
2
a
b
+...
Đọc tiếp
Chứng minh các đẳng thức sau: a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = a v ớ i a + b > 0 v à b ≠ 0
Biến đổi vế trái:
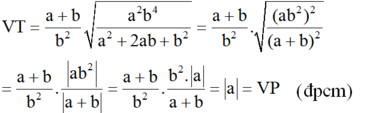
(vì a + b > 0 nên |a + b| = a + b; b2 > 0)
Đúng 0
Bình luận (0)