 mn ơi giúp em bài này với ạ,e đang cần gấp lắm
mn ơi giúp em bài này với ạ,e đang cần gấp lắm

Những câu hỏi liên quan
mn ơi ai thấy bài này giúp em được ko ạ,e đang cần gấp lắm
Đọc tiếp
mn ơi ai thấy bài này giúp em được ko ạ,e đang cần gấp lắm
a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC
Đúng 0
Bình luận (2)
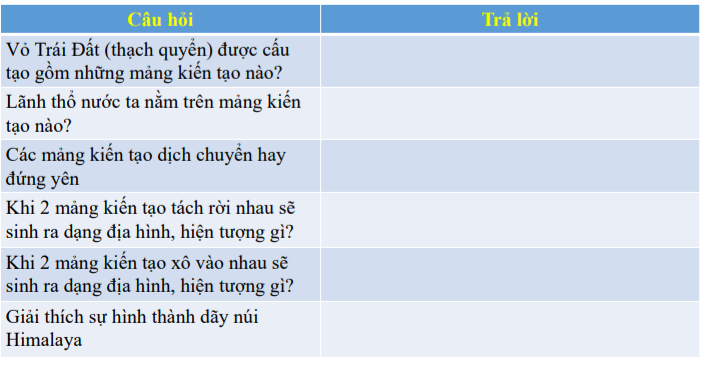 Mn giúp e bài này với ạ.E đang cần gấp lắm ạ.
Mn giúp e bài này với ạ.E đang cần gấp lắm ạ.
 Mn giúp e bài này với ạ.E đang cần gấp lắm ạ.
Mn giúp e bài này với ạ.E đang cần gấp lắm ạ.![]()
giúp em mấy bài này với mn,em đang cần gấp lắm ạ 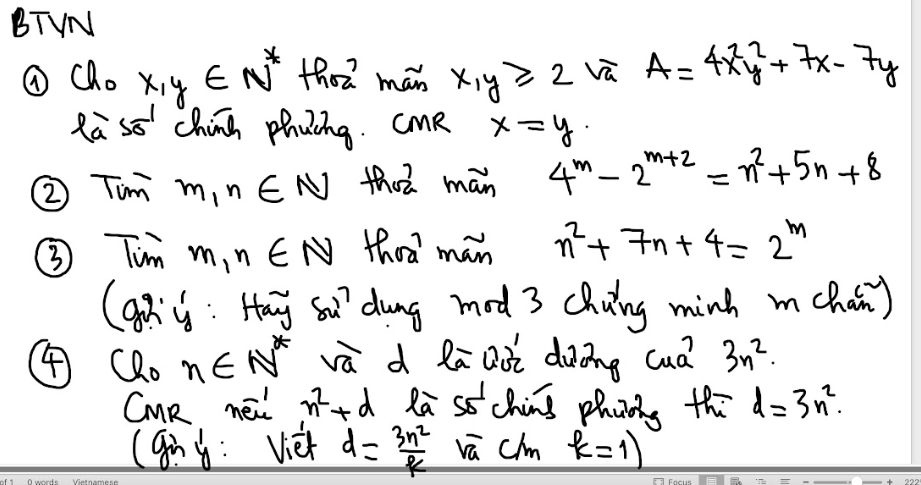
- Đây có phải là toán lớp 8 nữa không vậy :)? Mình học toán nâng cao nhưng chưa bao giờ thấy dạng này :).
Đúng 1
Bình luận (4)
b1:
do x;y thuộc số nguyên N và x,y\(\ge\)2
=>\(-4xy+1< +7x-7y< 4xy+1\)
\(\Rightarrow4x^2y^2-4xy+1< 4x^2y^2+7x-7y< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< 4x^2y^2+7x-7y< \left(2xy+1\right)^2\)
mà \(4x^2y^2+7x-7y\) là số chính phương và 1<2xy-1<2xy-1 nên ta có:
\(4x^2y^2+7x-7y-\left(2xy\right)^2\Leftrightarrow x=y\)
Đúng 2
Bình luận (0)
1.
TH1: \(x>0\Rightarrow7\left(x-y\right)>0\Rightarrow A>4x^2y^2\)
\(4xy-7x+7y+1>4xy-8x+7y+1=4x\left(y-2\right)+7y+1>0\) do \(x;y\ge2\)
\(\Rightarrow4xy+1>7x-7y\Rightarrow A< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy\right)^2< A< \left(2xy+1\right)^2\)
\(\Rightarrow A\) nằm giữa 2 SCP liên tiếp nên ko thể là SCP
TH2: \(x< y\) , tương tự ta có: \(7\left(x-y\right)< 0\Rightarrow A< 4x^2y^2\)
\(4xy+7x-7y-1>4xy+7x-8y-1=4y\left(x-2\right)+\left(7x-1\right)>0\)
\(\Rightarrow7x-7y>-4xy+1\Rightarrow A>4x^2y^2-4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< A< \left(2xy\right)^2\)
\(\Rightarrow A\) ko thể là SCP
TH3: \(x=y\Rightarrow A=\left(2xy\right)^2\) là SCP (thỏa mãn)
Vậy \(x=y\)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi, giúp em nhanh bài này với ạ, em đang cần gấp lắm ạ. Em cảm ơn rất nhiều ạ!!!!!

Mn giúp em bài này với ạ chỉ là sắp xếp từ lại thành một cậu thôi bài 29 với 30 mn không cần làm đâu ạ mong cao nhân nào giúp đỡ chứ em đang cần gấp lắm ạ
Đọc tiếp
Mn giúp em bài này với ạ chỉ là sắp xếp từ lại thành một cậu thôi bài 29 với 30 mn không cần làm đâu ạ mong cao nhân nào giúp đỡ chứ em đang cần gấp lắm ạ ![]()

what is her mother going to prepare for her bỉthdat party
Đúng 2
Bình luận (0)
there are three sticks of butter in the cupboard
Đúng 2
Bình luận (0)
i have enough food for the first three day of your stay
Đúng 2
Bình luận (1)
Mọi người ơi giúp em giải bài này với em cần gấp lắm, em cảm ơn trc vì đã giúp e ạ!!
Mn ơi giúp e bài này với ạ, e cần gấp lắm. E sắp thi cuối năm r ạ hmu-
\(\dfrac{1}{9+x}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
E cảm ơn mn nhìu lắm!!! Mọng mn giải chi tiết cho e hiểu ạ hyhy XĐ
ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}
Đúng 2
Bình luận (0)
Anh chị ơi giúp em làm bài này với ạ! E đg cần gấp lắm luôn ý:(( E cảm ơn anh chị nhiều ạ<3

\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
Đúng 2
Bình luận (1)
Bào quan riboxom trong chất tế bào có chức năng gì?
Đúng 0
Bình luận (0)
a) \(=\left(x^2+x\right)+\left(4x+4\right)=x\left(x+1\right)+4\left(x+1\right)=\left(x+1\right)\left(x+4\right)\)
b) \(=\left(x^2+2x\right)-\left(3x+6\right)=x\left(x+2\right)-3\left(x+2\right)=\left(x+2\right)\left(x-3\right)\)
c) \(=\left(x^2-2x\right)-\left(3x-6\right)=x\left(x-2\right)-3\left(x-2\right)=\left(x-2\right)\left(x-3\right)\)
d) \(3x^2+9x-30=3\left(x^2+3x-10\right)=3\left[\left(x^2+5x\right)-\left(2x+10\right)\right]=3\left[x\left(x+5\right)-2\left(x+5\right)\right]=3\left(x-2\right)\left(x+5\right)\)
e) \(=-\left(3x^2-5x-2\right)=-\left[\left(3x^2-6x\right)+\left(x-2\right)\right]=-\left[3x\left(x-2\right)+\left(x-2\right)\right]=-\left(3x+1\right)\left(x-2\right)\)
f) \(x^2-7x+6=\left(x^2-x\right)-\left(6x-6\right)=x\left(x-1\right)-6\left(x-1\right)=\left(x-1\right)\left(x-6\right)\)
h) \(=4\left(x^2-9x+14\right)=4\left[\left(x^2-7x\right)-\left(2x-14\right)\right]=4\left[x\left(x-7\right)-2\left(x-7\right)\right]=4\left(x-2\right)\left(x-7\right)\)
i) \(=3\left(3x^2-8x+5\right)=3\left[\left(3x^2-3x\right)-\left(5x-5\right)\right]=3\left[3x\left(x-1\right)-5\left(x-1\right)\right]=3\left(x-1\right)\left(3x-5\right)\)
k) \(=-\left(2x^2+5x+2\right)=-\left[\left(2x^2+4x\right)+\left(x+2\right)\right]=-\left[2x\left(x+2\right)+\left(x+2\right)\right]=-\left(x+2\right)\left(2x+1\right)\)
l) \(=\left(x^2-5xy\right)-\left(2xy-10y^2\right)=x\left(x-5y\right)-2y\left(x-5y\right)=\left(x-5y\right)\left(x-2y\right)\)
m) \(=\left(x^2-2xy\right)-\left(xy-2y^2\right)=x\left(x-2y\right)-y\left(x-2y\right)=\left(x-2y\right)\left(x-y\right)\)
n) \(=\left(x^2-3xy\right)+\left(xy-3y^2\right)=x\left(x-3y\right)+y\left(x-3y\right)=\left(x+y\right)\left(x-3y\right)\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Mn ơi giúp e bài này với ạ, e cần gấp lắm. E sắp thi cuối năm r ạ hmu-
\(\dfrac{x+2}{2019}+\dfrac{x+3}{2018}=\dfrac{x+4}{2017}+\dfrac{x}{2021}\)
E cảm ơn mn nhìu lắm!!! Mọng mn giải chi tiết cho e hiểu ạ hyhy XĐ
Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
Đúng 3
Bình luận (0)
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....
Đúng 2
Bình luận (0)