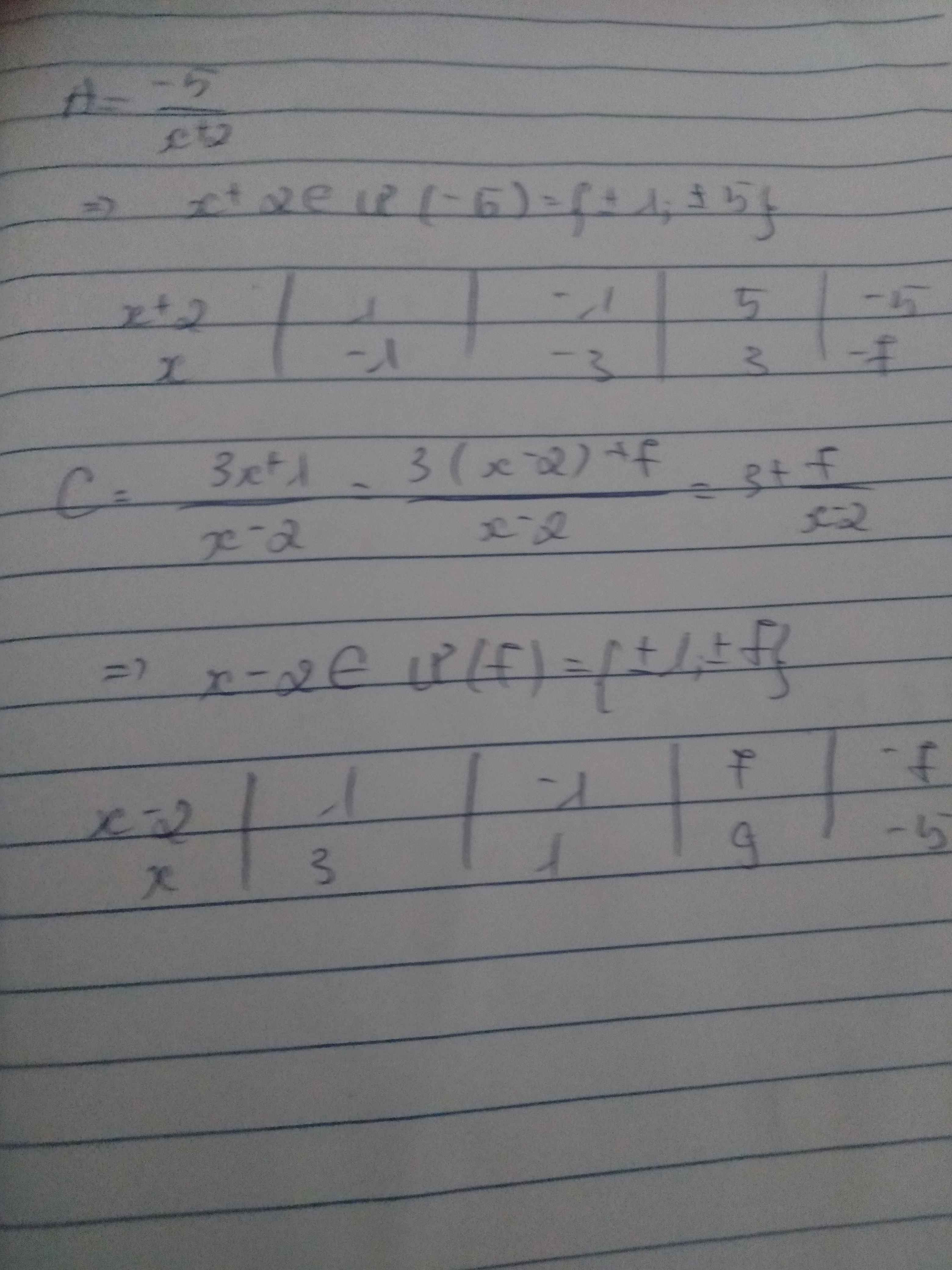a: \(A=\dfrac{x^2-5x+6-x^2+x+2x^2-6}{x\left(x-3\right)}=\dfrac{2x^2-4x}{x\left(x-3\right)}=\dfrac{2x}{x-3}\)

a, `2/(x-1) in ZZ`.

`=> 2 vdots x - 1`

`=> x-1 in Ư(2)`

`=> x - 1 in {+-1, +-2}`.

`=> x - 1 = 1 => x = 2`.

`=> x - 1 = -1 => x = 0`.

`=> x - 1 = -2 => x = -1`.

`=> x - 1 = 2 => x = 3`.

Vậy `x = 2, 0, - 1, 3`.

b, `4/(2x-1) in ZZ`

`=> 4 vdots 2x - 1`.

`=> 2x - 1 in Ư(4)`

Vì `2x vdots 2 => 2x - 1 cancel vdots 2`

`=> 2x - 1 in {+-1}`

`=> 2x - 1 = -1 => x = 0`.

`=> 2x - 1 = 1 => x = 1`

Vậy `x = 0,1`.

c, `(x+3)/(x-1) in ZZ`.

`=> x + 3 vdots x - 1`

`=> x - 1 + 4 vdots x - 1`.

`=> 4 vdots x-1`

`=> x -1 in Ư(4)`

`=> x - 1 in{+-1, +-2, +-4}`

`x - 1  = 1 => x = 2`.

`x - 1 = -1 => x = 0`.

`x - 1 = 2 =>x = 3`.

`x - 1 = -2 => x = -1`.

`x - 1 = 4 => x = 5`.

`x - 1 = -4 => x = -3`.

Vậy `x = 2, 0 , +-1, 5, -3`.

\(a.\)

\(\dfrac{x}{2}=\dfrac{y}{5}\)

Áp dụng tính chất dãy tỉ số bằng nhau : 

\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{35}{7}=5\)

\(\Rightarrow x=5\cdot2=10\\ y=5\cdot5=25\)

\(b.\)

\(\dfrac{x+2}{y+10}=\dfrac{1}{5}\)

\(\Leftrightarrow\dfrac{x+2}{1}=\dfrac{y+10}{5}\)

\(\Leftrightarrow\dfrac{3x+6}{3}=\dfrac{y+10}{5}\)

Áp dụng tính chất dãy tỉ số bằng nhau : 

\(\Leftrightarrow\dfrac{3x+6}{3}=\dfrac{y+10}{5}=\dfrac{y+10-3x-6}{5-3}=\dfrac{2-4}{2}=-1\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x+6=-3\\y+10=-5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-15\end{matrix}\right.\)

\(c.\)

\(\dfrac{x}{4}=\dfrac{y}{5}\)

\(\Leftrightarrow\dfrac{2x}{8}=\dfrac{y}{5}\)

Áp dụng tính chất dãy tỉ số bằng nhau : 

\(\dfrac{2x}{8}=\dfrac{y}{5}=\dfrac{2x-y}{8-5}=\dfrac{15}{3}=5\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x=5\cdot8\\y=5\cdot5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\)

a) Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\)

mà x+y=35

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{35}{7}=5\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{2}=5\\\dfrac{y}{5}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=25\end{matrix}\right.\)

Vậy: (x,y)=(10;25)

b) Ta có: \(\dfrac{x+2}{y+10}=\dfrac{1}{5}\)

nên \(\dfrac{x+2}{1}=\dfrac{y+10}{5}\)

hay \(\dfrac{3x+6}{3}=\dfrac{y+10}{5}\)

mà y-3x=2 

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{3x+6}{3}=\dfrac{y+10}{5}=\dfrac{y-3x+10-6}{5-3}=\dfrac{2+4}{2}=3\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{3x+6}{3}=3\\\dfrac{y+10}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+6=9\\y+10=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)

Vậy: (x,y)=(1;5)

c) Ta có: \(\dfrac{x}{4}=\dfrac{y}{5}\)

nên \(\dfrac{2x}{8}=\dfrac{y}{5}\)

mà 2x-y=15

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{2x}{8}=\dfrac{y}{5}=\dfrac{2x-y}{8-5}=\dfrac{15}{3}=5\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{4}=5\\\dfrac{y}{5}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\)

Vậy: (x,y)=(20;25)

a) Ta có: \(A=\dfrac{2x}{x+3}+\dfrac{x+1}{x-3}+\dfrac{3-11x}{9-x^2}\)

\(=\dfrac{2x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{11x-3}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{2x^2-6x+x^2+4x+3+11x-3}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{3x^2+9x}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{3x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x}{x-3}\)

b)

ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)

Ta có: P=AB

\(=\dfrac{3x}{x-3}\cdot\dfrac{x-3}{x+1}\)

\(=\dfrac{3x}{x+1}\)

Để \(P=\dfrac{9}{2}\) thì \(\dfrac{3x}{x+1}=\dfrac{9}{2}\)

\(\Leftrightarrow9\left(x+1\right)=6x\)

\(\Leftrightarrow9x-6x=-9\)

\(\Leftrightarrow3x=-9\)

hay x=-3(loại)

Vậy: Không có giá trị nào của x để \(P=\dfrac{9}{2}\)

a,\(\dfrac{6}{2x+1}=\dfrac{2}{7}\)

⇒\(\dfrac{6}{2x+1}=\dfrac{6}{21}\)

⇒\(2x+1=21\)

\(2x=21-1\)

\(2x=20\)

⇒\(x=10\)

a) 2ˣ + 2ˣ⁺³ = 72

2ˣ.(1 + 2³) = 72

2ˣ.9 = 72

2ˣ = 72 : 9

2ˣ = 8

2ˣ = 2³

x = 3

b) Để số đã cho là số nguyên thì (x - 2) ⋮ (x + 1)

Ta có:

x - 2 = x + 1 - 3

Để (x - 2) ⋮ (x + 1) thì 3 ⋮ (x + 1)

⇒ x + 1 ∈ Ư(3) = {-3; -1; 1; 3}

⇒ x ∈ {-4; -2; 0; 2}

Vậy x ∈ {-4; -2; 0; 2} thì số đã cho là số nguyên

c) P = |2x + 7| + 2/5

Ta có:

|2x + 7| ≥ 0 với mọi x ∈ R

|2x + 7| + 2/5 ≥ 2/5 với mọi x ∈ R

Vậy GTNN của P là 2/5 khi x = -7/2

a: Để D là số nguyên thì \(x-3\in\left\{1;-1;5;-5\right\}\)

hay \(x\in\left\{4;2;8;-2\right\}\)

ĐKXĐ: \(x\ne\pm1;x\ne0\)

a)\(\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right):\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\left(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\right):\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{x^2+2x+1-\left(x^2-2x+1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{4x}{\left(x-1\right)\left(x+1\right)}:\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{4x}{\left(x-1\right)\left(x+1\right)}.\dfrac{5\left(x-1\right)}{2x}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{10}{x+1}-\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)^2}\)

\(=\dfrac{10}{x+1}-\dfrac{x-1}{x+1}\)

\(=\dfrac{11-x}{x+1}\)

b) \(A=\dfrac{11-x}{x+1}=2\)

\(\Leftrightarrow11-x=2\left(x+1\right)\)

\(\Leftrightarrow11-x=2x+2\)

\(\Leftrightarrow-x-2x=2-11\)

\(\Leftrightarrow-3x=-9\)

\(\Leftrightarrow x=3\left(nhận\right)\)

c) -Để \(A=\dfrac{11-x}{x+1}\in Z\) thì:

\(\left(11-x\right)⋮\left(x+1\right)\)

\(\Rightarrow\left(12-x-1\right)⋮\left(x+1\right)\)

\(\Rightarrow12⋮\left(x+1\right)\)

\(\Rightarrow\left(x+1\right)\inƯ\left(12\right)\)

\(\Rightarrow\left(x+1\right)\in\left\{1;2;3;4;6;12;-1;-2;-3;-4;-6;-12\right\}\)

\(\Rightarrow x\in\left\{2;3;5;11;-2;-3;-4;-5;-7;-13\right\}\)