 giải hộ câu b)
giải hộ câu b)

Những câu hỏi liên quan
Giải hộ mk câu a với câu b
giải nhanh hộ tớ câu b
\(p=d\cdot h=10000\cdot\left(1,5-0,6\right)=9000Pa\)
Độ cao mực dầu:
\(h'=\dfrac{1}{3}h=\dfrac{1}{3}\cdot1,5=0,5m\)
\(\Rightarrow p=d_n\cdot h_n+d_d\cdot h_d=10000\cdot\left(1,5-0,5\right)+8000\cdot0,5=14000Pa\)
Đúng 3
Bình luận (1)
giải bài 2 câu b hộ mình chỉ câu b thôi nha vẽ hình luôn


giải hộ e câu b vs ạ
b: PTHĐGĐ là;
ax^2=2
=>ax^2-2=0
Δ=0^2-4*a*(-2)=8a
Để (P) cắt (d) tại hai điểm pb thì 8a>0
=>a>0
=>x=căn 2/a hoặc x=-căn 2/a
=>vecto OA=(căn 2/a;0); vecto OB=(-căn 2/a;0); vecto AB=(2*căn 2/a;2)
Theo đề, ta có: vecto OA*vecto OB=0 hoặc vecto OA*vecto AB=0 hoặc vecto OB*vecto AB=0
=>-2*căn 2/a+2=0 hoặc 2*căn 2/a+2=0
=>căn 2/a=1
=>a=2
Đúng 0
Bình luận (0)
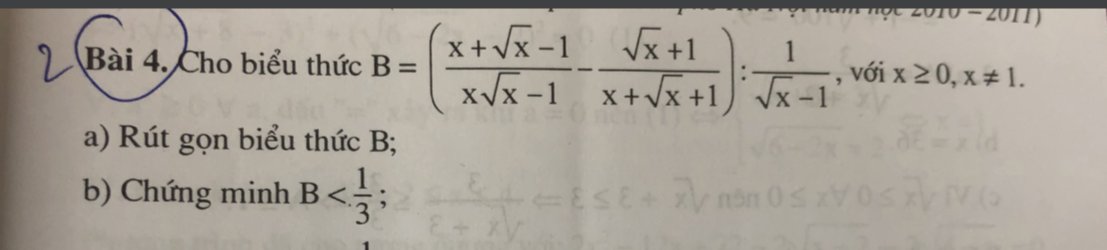
giải hộ mik câu b vs ạ
a: \(B=\dfrac{x+\sqrt{x}-1-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
b: \(B-\dfrac{1}{3}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{3}\)
\(=\dfrac{3\sqrt{x}-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(\sqrt{x}+1\right)^2}{3\left(x+\sqrt{x}+1\right)}< 0\)
=>B<1/3
Đúng 0
Bình luận (0)

giải hộ mình câu b th ạ
cho (o AB/2)lấy C thuộc đường tròn sao cho AC= R lấy D thuộ cung BC nhỏ .E là giao điểm cuẩD với BC vẽ dt đi qua E và vuông góc với AB tại H cắt AC tại F chứng minh tứ giác BHCF nội tiếp b) HA.HB=HE.HF
Đúng 0
Bình luận (1)
Ptr `(1)` có `2` nghiệm pb`<=>\Delta > 0`
`<=>[-(2m+1)]^2-4.2m > 0`
`<=>4m^2+4m+1-8m > 0`
`<=>4m^2-4m+1 > 0 <=>(2m-1)^2 > 0`
`<=>2m-1 \ne 0<=>m \ne 1/2`
Với `m \ne 1/2`, áp dụng Vi-ét có:`{(x_1+x_2=[-b]/a=2m+1),(x_1.x_2=c/a=2m):}`
Ta có:`T=x_1 ^2+x_2 ^2-x_1.x_2`
`<=>T=(x_1+x_2)^2-3x_1.x_2`
`<=>T=(2m+1)^2-3.2m`
`<=>T=4m^2+4m+1-6m`
`<=>T=4m^2-2m+1`
`<=>T=4m^2-2.2m+1/2+1/4+3/4`
`<=>T=(2m-1/2)^2+3/4`
Vì `(2m-1/2)^2 >= 0 AA m \ne 1/2`
`<=>(2m-1/2)^2+3/4 >= 3/4 AA m \ne 1/2`
Hay `T >= 3/4 AA m \ne 1/2`
Dấu "`=`" xảy ra`<=>(2m-1/2)^2=0<=>m=1/4` (t/m)
Vậy `GTN N` của `T` là `3/4` khi `m=1/4`
Đúng 3
Bình luận (0)
Giải hộ em phần b câu 2 và cả câu 3 với ạ🥺
ai giải hộ e câu b zới ak

giải kĩ hộ e câu b ak đừng lm ngắn gọn quá
Đúng 0
Bình luận (0)
b: Xét ΔAHC vuông tại H có
\(AH^2+HC^2=AC^2\)
nên \(AC^2-HC^2=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AH^2=AN\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AC=AC^2-HC^2\)
Đúng 1
Bình luận (0)
Mn giải hộ mình câu b bài 4 với !!


ai giải hộ mình câu b với c với
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)EB tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
=>BF\(\perp\)FC tại F
=>BF\(\perp\)AC tại F
Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp đường tròn đường kính AH
tâm K là trung điểm của AH
b:
Ta có: OE=OC
=>ΔOEC cân tại O
=>\(\widehat{OEC}=\widehat{OCE}\)
Ta có: ΔKHE cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
\(\widehat{KEO}=\widehat{KEC}+\widehat{OEC}\)
\(=\widehat{OCE}+\widehat{KHE}\)
\(=\widehat{ECB}+\widehat{DHC}=90^0\)
=>KE là tiếp tuyến của (O)
Xét ΔKEO và ΔKFO có
KE=KF
EO=FO
KO chung
Do đó: ΔKEO=ΔKFO
=>\(\widehat{KEO}=\widehat{KFO}=90^0\)
Ta có: \(\widehat{KEO}=\widehat{KFO}=\widehat{KDO}=90^0\)
=>K,E,O,F,D cùng thuộc đường tròn đường kính KO(ĐPCM)
Đúng 0
Bình luận (0)

















