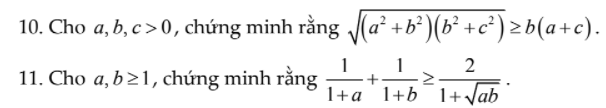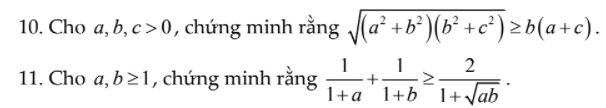a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)EB tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
=>BF\(\perp\)FC tại F
=>BF\(\perp\)AC tại F
Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp đường tròn đường kính AH
tâm K là trung điểm của AH
b:
Ta có: OE=OC
=>ΔOEC cân tại O
=>\(\widehat{OEC}=\widehat{OCE}\)
Ta có: ΔKHE cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
\(\widehat{KEO}=\widehat{KEC}+\widehat{OEC}\)
\(=\widehat{OCE}+\widehat{KHE}\)
\(=\widehat{ECB}+\widehat{DHC}=90^0\)
=>KE là tiếp tuyến của (O)
Xét ΔKEO và ΔKFO có
KE=KF
EO=FO
KO chung
Do đó: ΔKEO=ΔKFO
=>\(\widehat{KEO}=\widehat{KFO}=90^0\)
Ta có: \(\widehat{KEO}=\widehat{KFO}=\widehat{KDO}=90^0\)
=>K,E,O,F,D cùng thuộc đường tròn đường kính KO(ĐPCM)








 !
!