tìm giá trị nhỏ nhất cuả A=x^2+2y^2+2xy-2x+2018_6y

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của biểu thức: \(A=x^2+2y^2+2xy+2x-4y+2028\)
\(A=x^2+2x\left(y+1\right)+\left(y+1\right)^2-\left(y+1\right)^2+2y^2-4y+2028\)
\(=\left(x+y+1\right)^2-y^2-2x-1+2y^2-4y+2028\)
\(=\left(x+y+1\right)^2-6x+y^2+2027\)
\(=\left(x+y+1\right)+\left(y-3\right)^2+2018\ge2018\forall x;y\) (do...)
=> MinA = 2018 \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\y=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
tìm giá trị nhỏ nhất của A= x^2+2y^2+2xy-2x-8y+2017
Tìm giá trị nhỏ nhất của
A) x^2+2y^2-2xy+2x-10y
Ta thấy x2x2 và y2y2 luôn lớn hơn hoặc bằng 0 với mọi x
Nên để A đạt GTNN thì x = 0 và y = 0, do đó A = 0 + 0 - 0 + 0 - 0 = 0
Vậy Min A = 0
Còn cách khác nữa như sau :
Nhập biểu thức vào máy : 2x + 4y - 2xy + 2x - 10y = 0 SHIFT SOLVE
Y? 0 =
Solve for X? 0 =
KQ ra Solve x = 0
Vậy Min A = 0 khi x = 0 và y = 0.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất: C= x^2 + 2y^2 - 2xy + 2x - y + 2
Tìm giá trị nhỏ nhất:
\(P=x^2-2xy+2y^2-2x+3y+3\)
\(P=x^2-2xy+2y^2-2x+3y+3\)
\(=x^2-2x\left(y+1\right)+\left(y+1\right)^2-\left(y+1\right)^2+2y^2+3y+3\)
\(=\left(x-y-1\right)^2+y^2+y+2\)
\(=\left(x-y-1\right)^2+\left(y+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\)
\(Vì\) \(\left(x-y-1\right)^2+\left(y+\dfrac{1}{2}\right)^2\ge0\forall x,y\)
\(MinP=\dfrac{7}{4}\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức sau A=x^2-2xy+2y^2+2x-10y+2033
\(A=x^2-2xy+y^2+2x-2y+1+y^2-8y+16+2016\)
\(A=\left(x-y\right)^2+2\left(x-y\right)+1+\left(y-4\right)^2+2016\)
\(A=\left(x-y+1\right)^2+\left(y-4\right)^2+2016\)
vì \(\left(x-y+1\right)^2\ge0\)
\(\left(y-4\right)^2\ge0\)
nên \(\left(x-y+1\right)^2+\left(y-4\right)^2+2016\ge2016\)
dấu bằng xảy ra \(\Leftrightarrow\hept{\begin{cases}x=3\\y=4\end{cases}}\)
vậy gtnn của bt là 2016 khi x=3;y=4
đề này của sở giáo dục và đào tạo tỉnh hà nam
Đúng 0
Bình luận (0)
mk chiu ban ak di thi mk cug vao caau day nhưng ko biet lam
Đúng 0
Bình luận (0)
Cho x , y nguyên . Tìm giá trị nhỏ nhất của biểu thức : S = \(x^2+2y^2+2x-2y+2xy+2026\)
\(S=\left(x^2+y^2+1+2xy+2x+2y\right)+\left(y^2-4y+4\right)+2021\)
\(S=\left(x+y+1\right)^2+\left(y-2\right)^2+2021\ge2021\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(-3;2\right)\)
Đúng 1
Bình luận (0)
tìm giá trị nhỏ nhất B= x^2 +2xy +y^2 +2x+2y+10
Ta có :\(B=x^2+2xy+y^2+2x+2y+10\)
\(=\left(x+y\right)^2+2\left(x+y\right)+10\)
\(=\left(x+y+1\right)^2+9\ge9\forall x,y\)
Dấu "=" xảy ra \(\Leftrightarrow x+y+1=0\)
\(\Leftrightarrow x+y=-1\)
Vậy \(MinB=9\Leftrightarrow x+y=-1\)
tìm giá trị nhỏ nhất của x^2+y^2+2x+2y+2xy+5?
Xem thêm câu trả lời













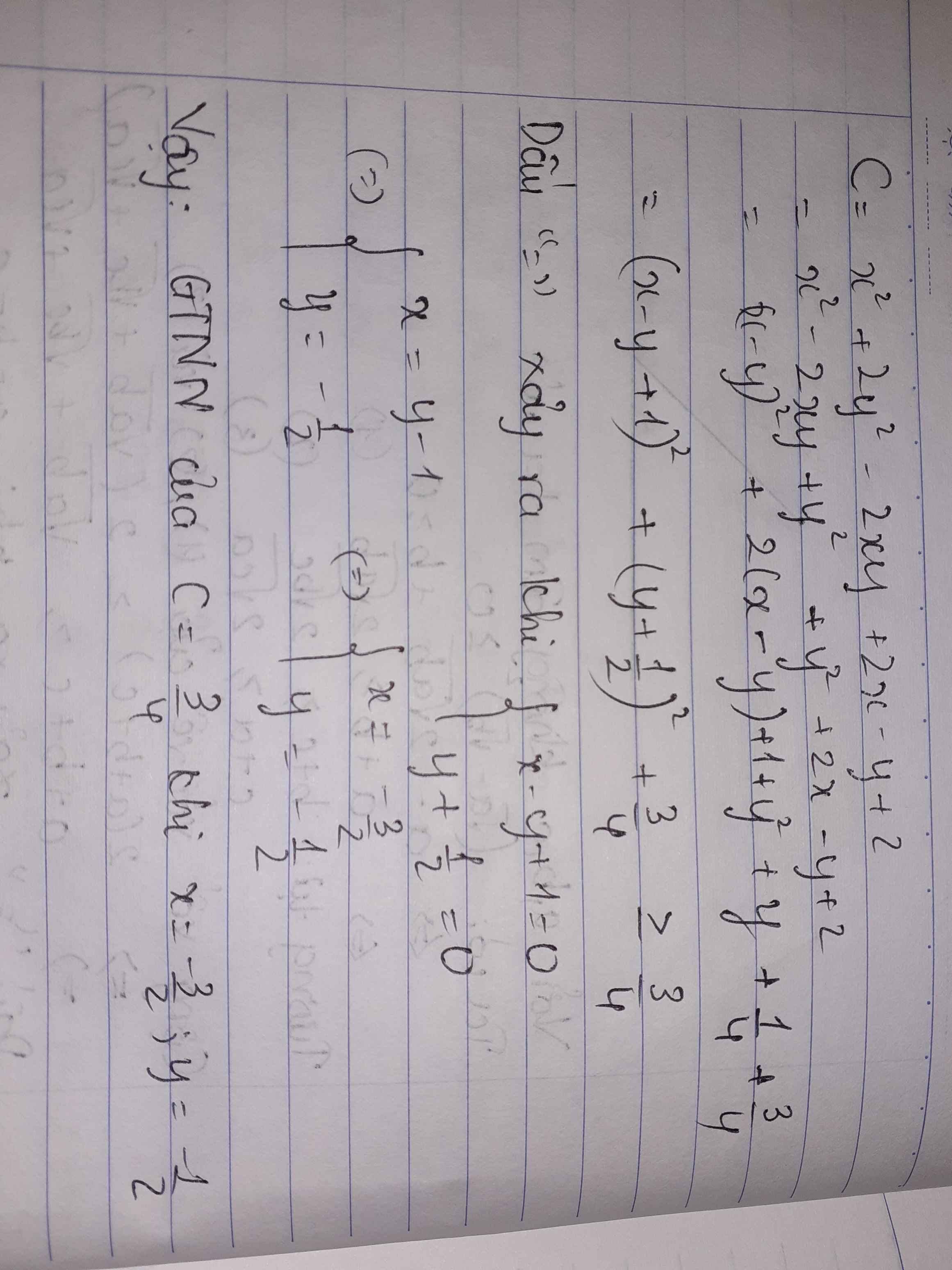










![Yuri Sweet[𝕿𝖊𝖆𝖒 𝕹𝖊𝖕𝖆𝖑]](https://hoc24.vn/images/avt/avt6428199_256by256.jpg)


