a) Vì \(\widehat A = 105^\circ  > 90^\circ \) nên là góc tù. Do đóc góc A là góc lớn nhất trong tam giác ABC

Cạnh BC đối diện với góc A nên là cạnh lớn nhất trong tam giác ABC

Vậy cạnh lớn nhất của tam giác ABC là cạnh BC.

b) Vì tam giác có góc A là góc tù

\( \Rightarrow \)Tam giác ABC là tam giác tù

\(\widehat{B}+\widehat{C}=140^0\)

\(\Leftrightarrow4\cdot\widehat{C}=140^0\)

\(\Leftrightarrow\widehat{C}=35^0\)

hay \(\widehat{B}=105^0\)

Vậy:  ΔABC tù

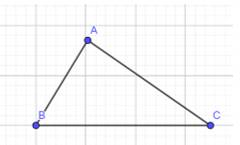
a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.

\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)

b) 

Theo định lí tổng 3 góc trong tam giác ABC, ta có:

\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)

 \( \Rightarrow\widehat C = \widehat B = {40^o}\)

\( \Rightarrow \) ABC là tam giác cân tại A.

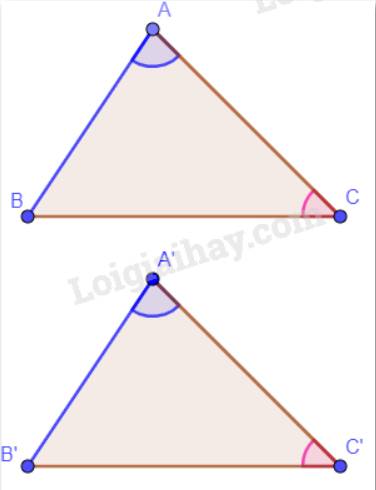
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).

Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).

Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)

Chọn A

A

chọn B vì A=N; M=C và B=P

 Kéo dài tia AO và đặt là Ax. Khi đó:

\(\widehat{BOC}=\widehat{BOx}+\widehat{COx}\)

 Xét tam giác OAB có \(\widehat{BOx}\) là góc ngoài tại O nên 

\(\widehat{BOx}=\widehat{A_1}+\widehat{ABO}\) (1)

 Tương tự, ta có \(\widehat{COx}=\widehat{A_2}+\widehat{ACO}\) (2)

 Cộng theo vế (1) và (2), ta được:

 \(\widehat{BOC}=\widehat{A_1}+\widehat{A_2}+\widehat{ABO}+\widehat{ACO}\)

        \(=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)

 Ta có đpcm.

A

B

D

Nhưng thực ra đây là tam giác đều

Có \(\widehat{B}=180^0-105^0-30^0=45^0\)

Kẻ AH vuông góc với BC

 \(\Rightarrow\Delta ABH\) là tam giác vuông cân tại A

\(\Rightarrow AH=BH\)

Có \(tanC=\dfrac{AH}{HC}\Leftrightarrow HC=\dfrac{AH}{tan30^0}=\sqrt{3}AH\)

\(\Rightarrow BH+CH=AH+\sqrt{3}AH\Leftrightarrow BC=\left(1+\sqrt{3}\right)AH\)\(\Leftrightarrow AH=\dfrac{BC}{1+\sqrt{3}}=\dfrac{2}{1+\sqrt{3}}\)

\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2}{1+\sqrt{3}}.2=\dfrac{2}{1+\sqrt{3}}\) (cm²)

Vậy...

a) Tam giác ABC có $\hat{A}$ = 100^{0 ,} $\hat{B}$ = 40⁰

Cạnh lớn nhất của tam giác ABC là BC vì BC đối diện với góc A và góc $\hat{A}$ = 100⁰ > 90⁰ nên góc A là góc tù

b) Tam giác ABC là tam giác tù