\(\begin{aligned} &\text { Điêu kiện }\left\{\begin{array}{l} 2 x+y \geq 0 \\ x-2 y+1 \geq 0 \end{array}\right.\\ &\text { Ta có hệ phương trình dã cho } \Leftrightarrow\left\{\begin{array}{l} 3 \sqrt{2 x+y}+\sqrt{x-2 y+1}=5 \\ 2 \sqrt{x-2 y+1}-(5 x+10 y)=9 \end{array}\right.\\ &\text { Đặt } u=\sqrt{2 x+y},(\mathrm{u} \geq 0) \text { và } v=\sqrt{x-2 y+1},(v \geq 0)\\ &\text { Suy ra }\left\{\begin{array}{l} 2 x+y=u^{2} \\ x-2 y+1=v^{2} \end{array} \Rightarrow\left\{\begin{array}{l} 2 x+y=u^{2} \\ x-2 y=v^{2}-1 \end{array}\right.\right.\\ &\text { Ta có } 5 x+10 y=m(2 x+y)+n(x-2 y), \text { suy ra }\left\{\begin{array}{l} 2 m+n=5 \\ m-2 n=10 \end{array} \Rightarrow\left\{\begin{array}{l} m=4 \\ n=-3 \end{array}\right.\right.\\ &\text { Vậy } 5 x+10 y=4(2 x+y)-3(x-2 y)=4 u^{2}-3\left(v^{2}-1\right) \end{aligned}\)

\(\text{Vậy ta có hệ phương trình}: \begin{array}{*{20}{l}} {\left\{ {\begin{array}{*{20}{l}} {3u + v = 5}\\ {2v - \left( {4{u^2} - 3{v^2} + 3} \right) = 9} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {v = 5 - 3u}\\ {4{u^2} - 3{v^2} - 2v + 12 = 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {v = 5 - 3u}\\ {23{u^2} - 96u + 73 = 0} \end{array}} \right. \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} u = 1\\ v = 2 \end{array} \right.\\ \left\{ \begin{array}{l} u = \dfrac{{73}}{{23}}\\ v = - \dfrac{{104}}{{23}} \end{array} \right. \end{array} \right.} \end{array}\)

\(\text{Trường hợp 1}: \left\{\begin{array}{l}u=1 \\ v=2\end{array} \Rightarrow\left\{\begin{array}{l}2 x+y=1 \\ x-2 y=3\end{array} \Leftrightarrow\left\{\begin{array}{l}x=1 \\ y=-1\end{array}\right. (tm) \right.\right.\\ \text{Trường hợp 2}: \left\{\begin{array}{l}u=\dfrac{73}{23} \\ v=-\dfrac{104}{23}\end{array}\right. (ktm \left.v \geq 0\right)\\ \text{Vậy hệ phương trình đã cho có nghiệm} \left\{\begin{array}{l}x=1 \\ y=-1\end{array}\right..\)

a) \(ĐK:y-2x+1\ge0;4x+y+5\ge0;x+2y-2\ge0,x\le1\)

Th1: \(\hept{\begin{cases}y-2x+1=0\\3-3x=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}0=0\\-1=\sqrt{10}-1\end{cases}}\)(không thỏa mãn)

Th2: \(x,y\ne1\)

\(2x^2-y^2+xy-5x+y+2=\sqrt{y-2x+1}-\sqrt{3-3x}\)\(\Leftrightarrow\left(x+y-2\right)\left(2x-y-1\right)=\frac{x+y-2}{\sqrt{y-2x+1}+\sqrt{3-3x}}\)\(\Leftrightarrow\left(x+y-2\right)\left(\frac{1}{\sqrt{y-2x+1}+\sqrt{3-3x}}+y-2x+1\right)=0\)

Dễ thấy \(\frac{1}{\sqrt{y-2x+1}+\sqrt{3-3x}}+y-2x+1>0\)nên x + y - 2 = 0

Thay y = 2 - x vào phương trình \(x^2-y-1=\sqrt{4x+y+5}-\sqrt{x+2y-2}\), ta được: \(x^2+x-3=\sqrt{3x+7}-\sqrt{2-x}\)\(\Leftrightarrow x^2+x-2=\sqrt{3x+7}-1+2-\sqrt{2-x}\)\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=\frac{3\left(x+2\right)}{\sqrt{3x+7}+1}+\frac{x+2}{2+\sqrt{2-x}}\)\(\Leftrightarrow\left(x+2\right)\left(\frac{3}{\sqrt{3x+7}+1}+\frac{1}{2+\sqrt{2-x}}+1-x\right)=0\)

Vì \(x\le1\)nên\(\frac{3}{\sqrt{3x+7}+1}+\frac{1}{2+\sqrt{2-x}}+1-x>0\)suy ra x = -2 nên y = 4

Vậy nghiệm của hệ phương trình là (x;y) = (-2;4)

b) \(\hept{\begin{cases}x^2+y^2=5\\x^3+2y^3=10x-10y\end{cases}}\Leftrightarrow\hept{\begin{cases}2\left(x^2+y^2\right)=10\left(1\right)\\x^3+2y^3=10\left(x-y\right)\left(2\right)\end{cases}}\)

Thay (1) vào (2), ta được: \(x^3+2y^3=2\left(x^2+y^2\right)\left(x-y\right)\Leftrightarrow\left(2y-x\right)\left(x^2+2y^2\right)=0\)

* Th1: \(x^2+2y^2=0\)(*)

Mà \(x^2\ge0\forall x;2y^2\ge0\forall y\Rightarrow x^2+2y^2\ge0\)nên (*) xảy ra khi x = y = 0 nhưng cặp nghiệm này không thỏa mãn hệ

* Th2: 2y - x = 0 suy ra x = 2y thay vào (1), ta được: \(y^2=1\Rightarrow y=\pm1\Rightarrow x=\pm2\) 

Vậy hệ có 2 nghiệm \(\left(x,y\right)\in\left\{\left(2;1\right);\left(-2;-1\right)\right\}\)

\(\left\{{}\begin{matrix}\sqrt{5x^2+2xy+2y^2}+\sqrt{2x^2+2xy+5y^2}=3\left(x+y\right)\\\sqrt{2x+y+1}+2\sqrt[3]{7x+12y+8}=2xy+y+5\end{matrix}\right.\)

Xét \(pt\left(1\right)\) dễ dàng suy ra \(x+y\ge0\)

\(VT=\sqrt{\left(x-y\right)^2+\left(2x+y\right)^2}+\sqrt{\left(x-y\right)^2+\left(2y+x\right)^2}\)

\(\ge\left|2x+y\right|+\left|2y+x\right|\ge3\left(x+y\right)\)

Đẳng thức xảy ra khi \(\left\{{}\begin{matrix}x=y\\x,y\ge0\end{matrix}\right.\)

Thay vào \(pt\left(2\right)\) ta được:

\(\sqrt{3x+1}+2\sqrt[3]{19x+8}=2x^2+x+5\)

\(\Leftrightarrow\left[\sqrt{3x+1}-\left(x+1\right)\right]+2\left[\sqrt[3]{19x+8}-\left(x+2\right)\right]=2x^2-2x\)

\(\Leftrightarrow\left(x-x^2\right)\left[\dfrac{1}{\sqrt{3x+1}+x+1}+2\cdot\dfrac{x+7}{\sqrt[3]{\left(19x+8\right)^2}+\left(x+2\right)\sqrt[3]{19x+8}+\left(x+2\right)^2}+2\right]=0\)

Do \(x;y\ge0\) nên pt trong ngoặc luôn dương

\(\Rightarrow x-x^2=0\Rightarrow x\left(1-x\right)=0\Rightarrow\)\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

Mà \(x=y\)\(\Rightarrow\left[{}\begin{matrix}x=y=0\\x=y=1\end{matrix}\right.\) là nghiệm của hpt

thanks b đã chỉ giúp mình.tại đánh máy nên mình ko để ý^^

pt(1): 5x²+2xy+2y²>=(2x+y)² nên \(\sqrt{5x^{2^{ }}+2xy+2y^2}\ge\:\)trị tuyệt đối 2x+y.

cmtt>\(\sqrt{2x^2+2xy+5y^2}\ge\)trị tuyệt đối x+ 2y.

>mà tt đối 2x+y cộng ttđ x+2y>= 3(x+y).

>(1)>=3(x+y).

đâu = xảy ra khi và chỉ khi x=y.

thay x=y >=0 vào (2):

\(\sqrt{3x+1}+2\sqrt[3]{19x+8}\) = 2x²+x+5.

<=>\(\left(\sqrt{3x+1}-\left(x+1\right)\right)\)+\(\left(2\sqrt[3]{19x+8}-\left(x+2\right)\right)\)= 2x²- 2x.

nhân liên hợp ta đc:

(x²-x)*(\(\dfrac{1}{\sqrt{3x+1}+x+1}+2\dfrac{x+7}{\sqrt[3]{19x+18}+\left(x+2\right)\left(\sqrt[3]{19x+18}\right)+\left(x+2\right)^2}=0\)

dễ thấy phần *>0 với mọi x,ytheo đk của (1)

>(x² -x)=0

>x=0 hoặc x=1

>(x,y)=(0,0); (1,1).

vậy....

\(\left\{{}\begin{matrix}\frac{2y-5x}{3}+5=\frac{y+27}{4}-2x\\\frac{x+1}{3}+y=\frac{6y-5x}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\frac{2y-5x}{3}+5+2x=\frac{y+27}{4}\\\frac{x+1}{3}+y=\frac{6y-5x}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\frac{2y+x+15}{3}=\frac{y+27}{4}\\\frac{x+3y+1}{3}=\frac{6y-5x}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8y+4x+60=3y+81\\7x+21y+7=18y-15x\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=21\\22x+3y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+5y=21\\66x+9y=-21\end{matrix}\right.\Leftrightarrow70x+14y=0\Leftrightarrow5x+y=0\Leftrightarrow20x+4y=0;4x+5y=21\Leftrightarrow20x+25y=105\Leftrightarrow\left(20x+25y\right)-\left(20x+4y\right)=105\Leftrightarrow21y=105\Leftrightarrow y=5.\text{Thay vào ta được:}4x+25=21\Leftrightarrow4x=-4\Leftrightarrow x=-1\)

\(\text{Thử lại ta thấy thỏa mãn: Vậy: x=-1;y=5}\)

\(\left\{{}\begin{matrix}\frac{2}{3}y-\frac{5}{3}x-\frac{1}{4}y+2x=\frac{27}{4}-5\\\frac{1}{3}x+\frac{5}{7}x+y-\frac{6}{7}y=-\frac{1}{3}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\frac{1}{3}x+\frac{5}{12}y=\frac{7}{4}\\\frac{22}{21}x+\frac{1}{7}y=-\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-1\\y=5\end{matrix}\right.\)

\(\left\{{}\begin{matrix}3x+2y=5\\2x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2y=5\\4x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\2x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=4\end{matrix}\right.\)

\(\left\{{}\begin{matrix}3x+2y=5\\2x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2y=5\\-4x-2y=-4\end{matrix}\right.\)

cộng từng vế của hệ pt ta có:

\(\Leftrightarrow-x=1\Leftrightarrow x=-1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\2x+y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\2\left(-1\right)+y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\-2+y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=4\end{matrix}\right.\)

vậy hệ pt có nghiệm \(\text{x=-1 }\)và \(y=4\)

2 x - y = 5 x + y + 2 x + 2 y - 5 = 0

Ta đưa về giải hai hệ phương trình:

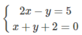
hoặc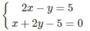 

Giải hệ:

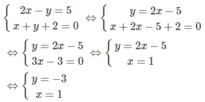
Giải hệ:

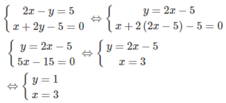
Vậy hệ phương trình đã cho có hai nghiệm

( x 1 ; y 1 ) = (1; -3) và ( x 2 ; y 2 ) = (3; 1)

a) \(\left\{{}\begin{matrix}2x+3y=5\\4x-5y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x+6y=10\\4x-5y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+3y=5\\11y=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+3\cdot\dfrac{9}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{27}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{28}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)

Vậy: \(x=\dfrac{14}{11};y=\dfrac{9}{11}\)