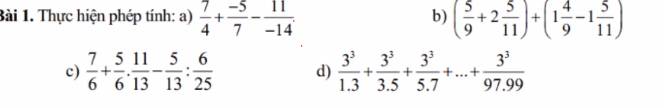 giúp e luôn với ạ
giúp e luôn với ạ

Những câu hỏi liên quan
Giúp em với mn ơi Giúp e làm luôn ạ
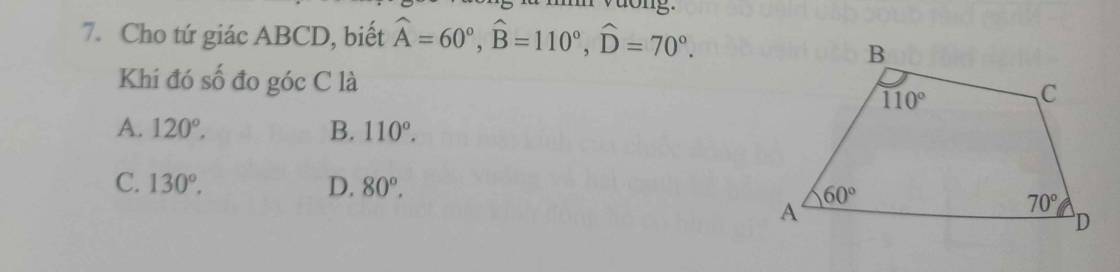 trình bày lời giải ra luôn ạ giúp e với ạ 🤧
trình bày lời giải ra luôn ạ giúp e với ạ 🤧
Xét tứ giác ABCD có:
A + B + C + D = 360 độ(theo định lý)
Suy ra C = 360 độ - ( A + B + D)
360 độ - 240 độ
120 độ
Vậy...
Đúng 0
Bình luận (1)

giúp e với, b 3,4 luôn ạ, lm cho e bài 3 trc ↑
giúp, đây ko phải thi nhoa, giải chi tiết mới tick
Đúng 0
Bình luận (0)
3.Chiều rộng là:
90x3/5=54(m)
Chu vi là:
(90+54)x2=288(m)
Diện tích là:
90x54=4860(m2)
ĐS:...
Đúng 3
Bình luận (5)
Câu 3 : lười làm
Câu 4: \(\left(\dfrac{3}{5}\times\dfrac{5}{3}\right)\times\left(\dfrac{5}{6}\times\dfrac{6}{5}\right)\times\dfrac{3}{4}=1\times1\times\dfrac{3}{4}=\dfrac{3}{4}\)
Đúng 2
Bình luận (2)
Xem thêm câu trả lời
giúp e với ạ. combo luôn cho gt nhaaa
Mn ơi giúp e với ạ bài khó lắm luôn :((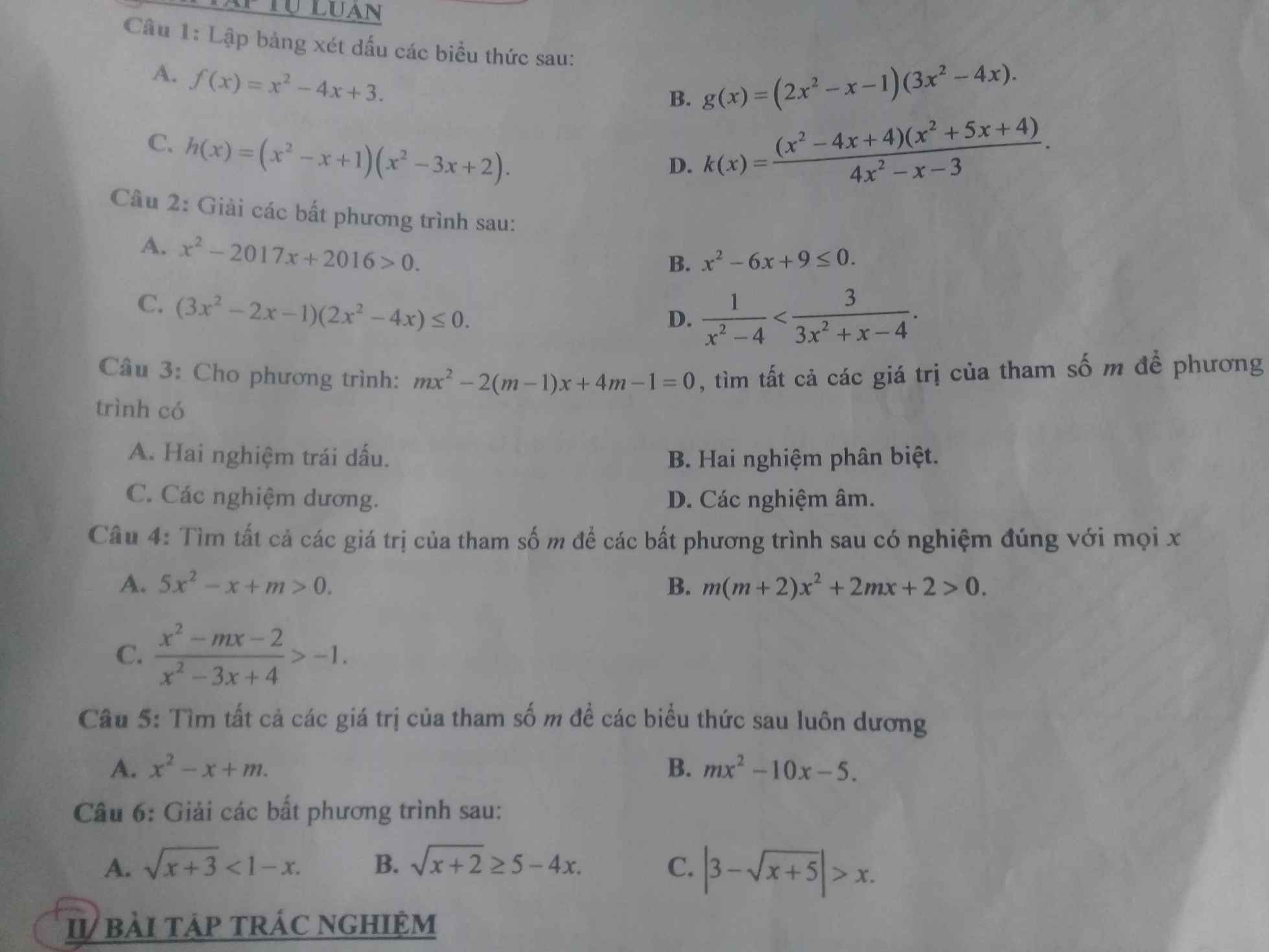
3.
TH1: \(m=0,pt\Leftrightarrow2x-1=0\Leftrightarrow x=\dfrac{1}{2}\)
TH2: \(m\ne0\)
a, Phương trình có hai nghiệm trái dấu khi \(m\left(4m-1\right)< 0\Leftrightarrow0< m< \dfrac{1}{4}\)
b, Phương trình có hai nghiệm phân biệt khi \(\Delta'=-3m^2-m+1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m< \dfrac{-1-\sqrt{13}}{6}\\m>\dfrac{-1+\sqrt{13}}{6}\end{matrix}\right.\)
c, Phương trình có hai nghiệm dương khi:
\(\left\{{}\begin{matrix}\Delta'>0\\x_1x_2>0\\x_1+x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -\dfrac{1+\sqrt{13}}{6}\\m>1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải thích luôn giúp e với ạ, em cảm ơn 
Anh chị giúp e câu toán 9 với ạ .Ngày mai e kt giữa kì r .Em cảm ơn rất nhiều luôn ạ
a: \(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{2\sqrt{x}+2+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}}{x-1}\)
Đúng 0
Bình luận (0)
\(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right).\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{2\left(\sqrt{x}+1\right)+\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{x+\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x-1}\)
\(\Rightarrow P=\dfrac{\sqrt{3+2\sqrt{2}}}{3+2\sqrt{2}-1}\)
\(\Rightarrow P=\dfrac{\sqrt{\left(\sqrt{2}+1\right)^2}}{2+2\sqrt{2}}\)
\(\Rightarrow P=\dfrac{\sqrt{2}+1}{2\left(\sqrt{2}+1\right)}\)
\(\Rightarrow P=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
(2x+1)^2+(2-x)(2x+1)<=0
giải BPT
giúp e với, e cần luôn ạ!
\(4x^2+4x+1+4x+2-2x^2-x\le0\)
\(\Leftrightarrow2x^2+7x+3\le0\Leftrightarrow\left(2x+1\right)\left(x+3\right)\le0\)
TH1 : \(\left\{{}\begin{matrix}2x+1\ge0\\x+3\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x\le-3\end{matrix}\right.\)<=> -1/2 =< x =< -3
TH2 : \(\left\{{}\begin{matrix}2x+1\le0\\x+3\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\x\ge-3\end{matrix}\right.\)( vô lí )
Đúng 0
Bình luận (0)
Giúp e với ạ, có bài giải luôn nha 🥺👉👈
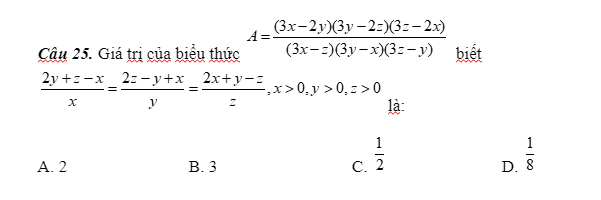
Áp dụng tc dtsbn:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\\ \Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.;\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2z\end{matrix}\right.\\ \Rightarrow P=\dfrac{xyz}{2x\cdot2y\cdot2z}=\dfrac{1}{8}\)
Chọn D
Đúng 5
Bình luận (1)
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
\(\Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.\) và \(\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2x\end{matrix}\right.\)
Thay vào A:
\(A=\dfrac{z.x.y}{2y.2z.2x}=\dfrac{1}{8}\)
Đúng 4
Bình luận (1)
Vì x>0, y>0, z>0 ⇒ x+y+z>0
Áp dụng t/c dtsbn ta có:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2y+z-x+2z-y+x+2x+y-z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
\(\dfrac{2y+z-x}{x}=2\Rightarrow2y+z-x=2x\Rightarrow2y+z=3x\\ \dfrac{2z-y+x}{y}=2\Rightarrow2z-y+x=2y\Rightarrow2z+x=3y\\ \dfrac{2x+y-z}{z}=2\Rightarrow2x+y-z=2z\Rightarrow2x+y=3z\)
\(A=\dfrac{\left(3x-2y\right)\left(3y-2z\right)\left(3z-2x\right)}{\left(3x-z\right)\left(3y-x\right)\left(3z-y\right)}\)
\(\Rightarrow A=\dfrac{\left(2y+z-2y\right)\left(2z+y-2z\right)\left(2x+y-2x\right)}{\left(2y+z-z\right)\left(2z+x-x\right)\left(2x+y-y\right)}\)
\(\Rightarrow A=\dfrac{xyz}{2x.2y.2z}\)
\(\Rightarrow A=\dfrac{1}{8}\)
Đúng 1
Bình luận (3)
Xem thêm câu trả lời
Anh chị ơi giúp em làm bài này với ạ! E đg cần gấp lắm luôn ý:(( E cảm ơn anh chị nhiều ạ<3

\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
Đúng 2
Bình luận (1)
Bào quan riboxom trong chất tế bào có chức năng gì?
Đúng 0
Bình luận (0)
a) \(=\left(x^2+x\right)+\left(4x+4\right)=x\left(x+1\right)+4\left(x+1\right)=\left(x+1\right)\left(x+4\right)\)
b) \(=\left(x^2+2x\right)-\left(3x+6\right)=x\left(x+2\right)-3\left(x+2\right)=\left(x+2\right)\left(x-3\right)\)
c) \(=\left(x^2-2x\right)-\left(3x-6\right)=x\left(x-2\right)-3\left(x-2\right)=\left(x-2\right)\left(x-3\right)\)
d) \(3x^2+9x-30=3\left(x^2+3x-10\right)=3\left[\left(x^2+5x\right)-\left(2x+10\right)\right]=3\left[x\left(x+5\right)-2\left(x+5\right)\right]=3\left(x-2\right)\left(x+5\right)\)
e) \(=-\left(3x^2-5x-2\right)=-\left[\left(3x^2-6x\right)+\left(x-2\right)\right]=-\left[3x\left(x-2\right)+\left(x-2\right)\right]=-\left(3x+1\right)\left(x-2\right)\)
f) \(x^2-7x+6=\left(x^2-x\right)-\left(6x-6\right)=x\left(x-1\right)-6\left(x-1\right)=\left(x-1\right)\left(x-6\right)\)
h) \(=4\left(x^2-9x+14\right)=4\left[\left(x^2-7x\right)-\left(2x-14\right)\right]=4\left[x\left(x-7\right)-2\left(x-7\right)\right]=4\left(x-2\right)\left(x-7\right)\)
i) \(=3\left(3x^2-8x+5\right)=3\left[\left(3x^2-3x\right)-\left(5x-5\right)\right]=3\left[3x\left(x-1\right)-5\left(x-1\right)\right]=3\left(x-1\right)\left(3x-5\right)\)
k) \(=-\left(2x^2+5x+2\right)=-\left[\left(2x^2+4x\right)+\left(x+2\right)\right]=-\left[2x\left(x+2\right)+\left(x+2\right)\right]=-\left(x+2\right)\left(2x+1\right)\)
l) \(=\left(x^2-5xy\right)-\left(2xy-10y^2\right)=x\left(x-5y\right)-2y\left(x-5y\right)=\left(x-5y\right)\left(x-2y\right)\)
m) \(=\left(x^2-2xy\right)-\left(xy-2y^2\right)=x\left(x-2y\right)-y\left(x-2y\right)=\left(x-2y\right)\left(x-y\right)\)
n) \(=\left(x^2-3xy\right)+\left(xy-3y^2\right)=x\left(x-3y\right)+y\left(x-3y\right)=\left(x+y\right)\left(x-3y\right)\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời































