Tìm hệ số của x^20 trong khai triển (1-x)^30

Những câu hỏi liên quan
Tìm hệ số của
x
7
trong khai triển
P
(
x
)
(
x
+
1
)
20
A.
C
20
7
B. ...
Đọc tiếp
Tìm hệ số của x 7 trong khai triển P ( x ) = ( x + 1 ) 20
A. C 20 7
B. A 20 7
C. A 20 13
D. P 7
Đáp án A
Phương pháp: Sử dụng khai triển nhị thức Newton:
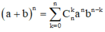
Cách giải:
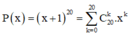
Để tìm hệ số của x 7 ta cho k = 7, khi đó hệ số của x 7 là C 20 7
Đúng 0
Bình luận (0)
1. Tìm hệ số của số hạng x^4 trong khai triển left(x-3right)^92. Tìm hệ số của số hạng chứa x^{12}y^{13} trong khai triển left(2x+3yright)^{25}3. Tìm hệ số của số hạng chứa x^4 trong khai triển left(dfrac{x}{3}-dfrac{3}{x}right)^{12}4. Tìm hệ số của số hạng không chứa x trong khai triển left(x^2-dfrac{1}{x}right)^65. Tìm hệ số của số hạng không chứa x trong khai triển left(x+dfrac{1}{x^4}right)^{10}
Đọc tiếp
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
15. Số hạng chính giữa trong khai triển (3x + 2y)^4 là?
18. Tìm hệ số của x^7 trong khai triển : h(x)= x(2 + 3x)^9 là?
19. Tìm hệ số của x^7 trong khai triển g(x)= (1+x)^7 + (1-x)^8 + (2+x)^9 là?
15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
Đúng 1
Bình luận (3)
Hệ số của x trong khai triển (x + 1/x) ^ 30
SHTQ là:
\(C^k_{30}\cdot x^{30-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_{30}\cdot x^{30-2k}\)
Hệ số của x^1 là 30-2k=1
=>k=29/2(loại)
=>Ko có x trong khai triển này
Đúng 3
Bình luận (0)
Tìm hệ số của
x
6
y
14
trong khai triển
(
x
+
5
y
)
20
A.
5
6
C
20
6
B.
5
14
C
20
14
...
Đọc tiếp
Tìm hệ số của x 6 y 14 trong khai triển ( x + 5 y ) 20
A. 5 6 C 20 6
B. 5 14 C 20 14
C. 5 6 C 20 14
D. 5 14
Số hạng chứa x6y14 trong khai triển (x+5y)20 là C2014.x6.(5y)14= 514.C2014.x6.y14 nên hệ số của x6y14 là 514. C2014
Chọn B
Đúng 0
Bình luận (0)
Hệ số của x^26 trong khai triển (x + 1/x) ^ 30
SHTQ là:
\(C^k_{30}\cdot x^{30-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_{30}\cdot x^{30-2k}\)
Số hạng của x^26 tương ứng với 30-2k=26
=>k=2
=>Hệ số là \(C^2_{30}\)
Đúng 0
Bình luận (0)
Biết tổng các hệ số của ba số hạng đầu trong khai triển \(\left(x^3+\dfrac{1}{x^2}\right)^n\) bằng 11. Tìm hệ số của \(x^7\) trong khai triển đó.
\(C_n^0+C_n^1+C_n^2=11\)
\(\Rightarrow1+n+\dfrac{n\left(n-1\right)}{2}=11\)
\(\Leftrightarrow n^2+n-20=0\Rightarrow\left[{}\begin{matrix}n=4\\n=-5\left(loại\right)\end{matrix}\right.\)
\(\left(x^3+\dfrac{1}{x^2}\right)^4\) có SHTQ: \(C_4^k.x^{3k}.x^{-2\left(4-k\right)}=C_4^k.x^{5k-8}\)
\(5k-8=7\Rightarrow k=3\)
Hệ số: \(C_4^3=4\)
Đúng 0
Bình luận (0)
Hệ số của x8 trong khai triển nhị thức (x+ 1/x)20 là
Lời giải:
Theo khai triển Newton:
\((x+\frac{1}{x})^{20}=\sum\limits_{k=0}^{20}C^k_{20}x^k(x^{-1})^{20-k}=\sum\limits_{k=0}^{20}C^k_{20}x^{2k-20}\)
$2k-20=8\Leftrightarrow k=14$
Hệ số của $x^8$ là: $C^{14}_{20}$
Đúng 0
Bình luận (0)
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x
2
-
2
x
n
C
n
0...
Đọc tiếp
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x 2 - 2 x n = C n 0 x 2 n + C n 1 x 2 n - 1 - 2 x + . . . + C n n - 1 x 2 - 2 x n - 1 + C n n - 2 x n n ∈ ℕ *
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. 11520
B. 11250
C. 12150
D. 10125
a)Tìm số hạng không chứa x trong khai triển (x+2/x)10
b)Tìm số hạng không chứa x trong khai triển (x+2/x2)6
c)Tìm hệ số của số hạng chứa x10 trong khai triển (3x3-2/x2)5
a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810
Đúng 1
Bình luận (0)
















