biến đổi thành hằng đẳng thức\(^{x^2+4x+4}\)

Những câu hỏi liên quan
Biến đổi thành hằng đẳng thức
\(\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{3-2\sqrt{3}+1}=\sqrt{\left(\sqrt{3}-1\right)^2}=\left|\sqrt{3}-1\right|=\sqrt{3}-1\)
Đúng 3
Bình luận (0)
biến đổi x^2-y^2 về hằng đẳng thức
\(x^2-y^2=\left(x-y\right)\left(x+y\right)\)
Đúng 1
Bình luận (0)
2: Viết lại các đa thức thành vế kia hằng đẳng thức:
a, 4x^(4)-4x^(2)+16
b, (x+2y)^(2).
c, 36+x^(2)-12xy
d, (x+5y)^(2).
e, 4x^(2)-12x+9
f,(x-2y)^(2).
\(4x^4-4x^2+1=\left(2x^2-1\right)^2\)
\(\left(x+2y\right)^2=x^2+4xy+4y^2\)
\(36-12x+x^2=\left(6-x\right)^2\)
\(\left(x+5y\right)^2=x^2+10xy+25y^2\)
\(4x^2-12x+9=\left(2x-3\right)^2\)
\(\left(x-2y\right)^2=x^2-4xy+4y^2\)
Đúng 0
Bình luận (0)
Biến đổi (theo hằng đẳng thức)
4b^2+a^2+4ab
-49-2a^4+14 căn 2 *a^2
`4b^2+a^2+4ab`
`=(2b)^2+2.2b.a+a^2`
`=(a+2b)^2`
`-49-2a^4+14sqrt2a^2`
`=-(2a^4-14sqrt2a^2+49)`
`=-((sqrt2a^2)^2-2.sqrt2a^2.7+7^2)`
`=-(sqrt2a^2-7)^2`
Đúng 2
Bình luận (0)
\(a^2+4ab+4b^2=\left(a+2b\right)^2\)
\(-49-2a^4+14\sqrt{2a^2}=-\left(\sqrt{2a^2}-7\right)^2\)
Đúng 1
Bình luận (1)
Điền các đơn thức vào chỗ để hoàn thành các hằng đẳng thức sau:a)
x
2
+ 4x + ...
(
x
+
.
.
.
)
2
; b) ...-12x + 9
(
2
x
-
.
....
Đọc tiếp
Điền các đơn thức vào chỗ để hoàn thành các hằng đẳng thức sau:
a) x 2 + 4x + ... = ( x + . . . ) 2 ; b) ...-12x + 9 = ( 2 x - . . . ) 2 ;
c) 4 x 2 +...+... ( 2 x - 3 y ) 2 ; d) x − . .. ( . .. + y 2 ) = . .. − y 2 4 .
Hoàn thiện HĐT ta thu được các đơn thức cần điền vào “…”.
a) x 2 + 4x + 4 = ( x + 2 ) 2 . b) 4 x 2 – 12x + 9 = ( 2 x – 3 ) 2 .
c) 4 x 2 – 12xy + 9 y 2 = ( 2 x – 3 y ) 2 .
Chú ý: phép trừ ta chuyển thành cộng đại số.
d) x − y 2 x + y 2 = x 2 − y 2 4 .
Đúng 0
Bình luận (0)
Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến đổi tích thành tổng và tổng thành tích.
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
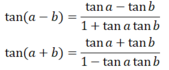
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
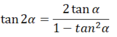
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
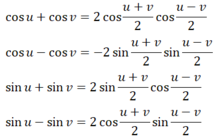
Đúng 0
Bình luận (0)
tìm x hằng đẳng thức x^2 4x +4=0
Mất dấu nên xét 2 th.
TH1
`x^2-4x+4=0`
`<=>x^2-2.x.2+2^2=0`
`<=>(x-2)^2=0`
`<=>x-2=0`
`<=>x=2`
`=>S={2}`
TH2
`x^2+4x+4=0`
`<=>x^2+2.x.2+2^2=0`
`<=>(x+2)^2=0`
`<=>x+2=0`
`<=>x=-2`
`=>S={-2}`
Đúng 0
Bình luận (0)
đề à -4x hay +4x nó sẽ ra kết quả khác nhau em ạ!
Đúng 0
Bình luận (1)
tìm x hằng đẳng thức x^2 +4x +4=0
`x^2+4x+4=0`
`⇔x^2+2.x.2+2^2=0`
`⇔(x+2)^2=0`
`⇔x+2=0⇔x=−2`
Vậy `x=-2`.
Đúng 2
Bình luận (0)
\(x^2+4x+4=x^2+2.2.x+2^2=\left(x+2\right)^2=0\Rightarrow x+2=0\Rightarrow x=-2\)
Đúng 3
Bình luận (1)
biến đổi về hằng đẳng thức:
( x + y - 1 )( x - y - 1)

























