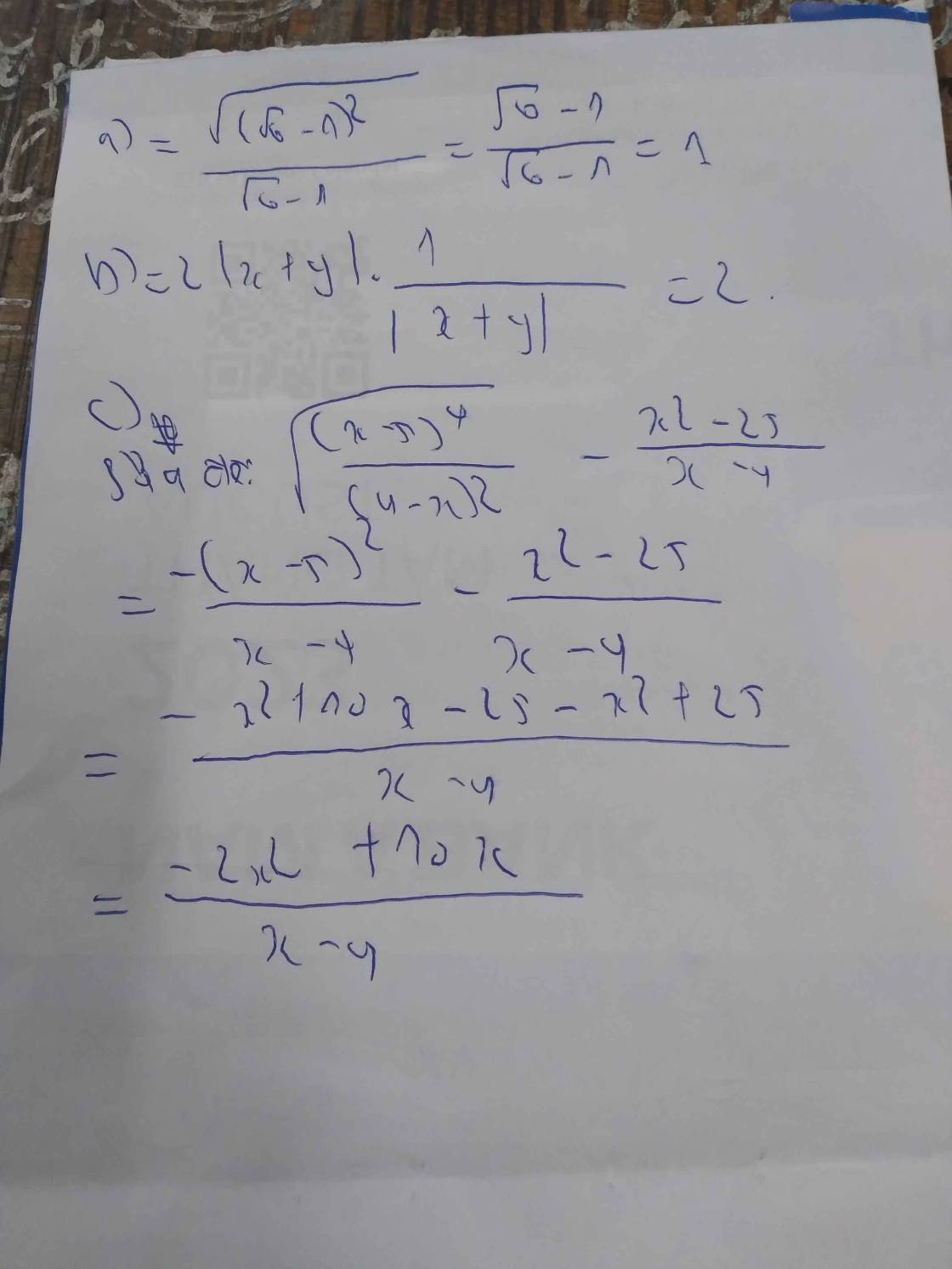Đk: \(\left\{{}\begin{matrix}y\ge0\\x>1\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\sqrt{9\left(x-1\right)y}=y\left(2+\sqrt{\dfrac{y}{x-1}}\right)\left(1\right)\\y^2+xy-5x+7=0\left(2\right)\end{matrix}\right.\)

Đặt \(\left\{{}\begin{matrix}a=\sqrt{\left(x-1\right)y}\left(a\ge0\right)\\b=\sqrt{\dfrac{y}{x-1}}\left(b\ge0\right)\end{matrix}\right.\)

\(\left(1\right)\Rightarrow3a=ab\left(2+b\right)\)

Với \(a=0\Rightarrow\sqrt{\left(x-1\right)y}=0\Rightarrow y=0\) (vì \(x\ne1\)).

Thay \(y=0\) vào (2) ta được:

\(2^2+x.2-5x+7=0\)

\(\Leftrightarrow x=\dfrac{11}{3}\left(nhận\right)\)

Với \(a\ne0\Rightarrow3=b\left(2+b\right)\)

\(\Leftrightarrow b^2+2b-3=0\)

\(\Leftrightarrow b^2-b+3b-3=0\)

\(\Leftrightarrow b\left(b-1\right)+3\left(b-1\right)=0\)

\(\Leftrightarrow\left(b-1\right)\left(b+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}b=1\left(nhận\right)\\b=-3\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow\sqrt{\dfrac{y}{x-1}}=1\Rightarrow x=y+1\)

Thay vào (2) ta được:

\(y^2+\left(y+1\right)y-5\left(y+1\right)+7=0\)

\(\Leftrightarrow y^2+y^2+y-5y-5+7=0\)

\(\Leftrightarrow2y^2-4y+2=0\)

\(\Leftrightarrow2\left(y-1\right)^2=0\)

\(\Leftrightarrow y=1\Rightarrow x=1+1=2\)

Vậy hệ phương trình đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(\dfrac{11}{3};0\right),\left(2;1\right)\right\}\)

Ai giúp mình với, mình cần sự giúp đỡ, mai nộp bài rồi

\(A=\dfrac{7\sqrt{a}}{a-9}-\left(\dfrac{\sqrt{a}}{\sqrt{a}-3}-\dfrac{\sqrt{a}-1}{\sqrt{a}+3}\right)=\dfrac{7\sqrt{a}}{a-9}-\dfrac{\sqrt{a}\left(\sqrt{a}+3\right)-\left(\sqrt{a}-1\right)\left(\sqrt{a}-3\right)}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}=\dfrac{7\sqrt{a}}{a-9}-\dfrac{a+3\sqrt{a}-a+3\sqrt{a}+\sqrt{a}-3}{a-9}=\dfrac{3}{a-9}\)\(B=\left(\dfrac{1}{\sqrt{a}-3}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+3}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-3}\right)=\dfrac{\sqrt{a}-\sqrt{a}+3}{\sqrt{a}\left(\sqrt{a}-3\right)}:\dfrac{a-9-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-3\right)}=\dfrac{3}{\sqrt{a}\left(\sqrt{a}-3\right)}.\dfrac{\left(\sqrt{a}-3\right)\left(\sqrt{a}-2\right)}{-5}=\dfrac{3\sqrt{a}-6}{-5\sqrt{a}}\)

\(C=\left(\dfrac{a\sqrt{a}}{\sqrt{a}-1}-\dfrac{a^2}{a\sqrt{a}-a}\right).\left(\dfrac{1}{a}-2\right)=\left(\dfrac{a\sqrt{a}}{\sqrt{a}-1}-\dfrac{a^2}{a\left(\sqrt{a}-1\right)}\right).\dfrac{1-2a}{a}=\dfrac{a\sqrt{a}-a}{\sqrt{a}-1}.\dfrac{1-2a}{a}=\dfrac{a\left(\sqrt{a}-1\right)}{\sqrt{a}-1}.\dfrac{1-2a}{a}=1-2a\)\(D=\dfrac{a\sqrt{a}+1}{a-1}-\dfrac{a-1}{\sqrt{a}+1}=\dfrac{a\sqrt{a}+1-\left(a-1\right)\left(\sqrt{a}-1\right)}{a-1}=\dfrac{a\sqrt{a}+1-a\sqrt{a}+a+\sqrt{a}-1}{a-1}=\dfrac{a+\sqrt{a}}{a-1}=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}=\dfrac{\sqrt{a}}{\sqrt{a}-1}\)

\(E=\dfrac{a}{a-4}+\dfrac{1}{\sqrt{a}-2}+\dfrac{1}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+2+\sqrt{a}-2}{a-4}=\dfrac{a+2\sqrt{a}}{a-4}=\dfrac{\sqrt{a}\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}=\dfrac{\sqrt{a}}{\sqrt{a}-2}\)

1) \(9^{x-1}=\dfrac{1}{9}\) (1)

\(\Leftrightarrow3^{2x-2}=3^{-2}\)

\(\Leftrightarrow2x-2=-2\)

\(\Leftrightarrow2x=0\)

\(\Leftrightarrow x=0\)

Vậy tập nghiệm phương trình (1) là \(S=\left\{0\right\}\)

2) \(\dfrac{1}{3}:\sqrt{7-3x^2}=\dfrac{2}{15}\) (2)

\(\Leftrightarrow\dfrac{1}{3}\cdot\dfrac{1}{\sqrt{7-3x^2}}=\dfrac{2}{15}\)

\(\Leftrightarrow\dfrac{1}{3\sqrt{7-3x^2}}=\dfrac{2}{15}\)

\(\Leftrightarrow15=6\sqrt{7-3x^2}\)

\(\Leftrightarrow6\sqrt{7-3x^2}=15\)

\(\Leftrightarrow\sqrt{7-3x^2}=\dfrac{5}{2}\)

\(\Leftrightarrow7-3x^2=\dfrac{25}{4}\)

\(\Leftrightarrow-3x^2=\dfrac{25}{4}-7\)

\(\Leftrightarrow-3x^2=-\dfrac{3}{4}\)

\(\Leftrightarrow x^2=\dfrac{1}{4}\)

\(\Leftrightarrow x=\pm\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)

Vậy tập nghiệm phương trình (2) là \(S=\left\{-\dfrac{1}{2};\dfrac{1}{2}\right\}\)

Ta có :

\(\left\{{}\begin{matrix}\sqrt{\left(x-\sqrt{2}\right)^2}\ge0\\\sqrt{\left(y+\sqrt{2}\right)^2}\ge0\\\left|x+y+z\right|\ge0\end{matrix}\right.\)

Mà \(\sqrt{\left(x-\sqrt{2}\right)^2}+\sqrt{\left(y+\sqrt{2}\right)^2}+\left|x+y+z\right|=0\\ \Rightarrow\left\{{}\begin{matrix}\sqrt{\left(x-\sqrt{2}\right)^2}=0\\\sqrt{\left(y+\sqrt{2}\right)^2}=0\\\left|x+y+z\right|=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\sqrt{2}\\y=-\sqrt{2}\\z=0\end{matrix}\right.\)

a: Ta có: \(\sqrt{4x+20}-3\sqrt{x+5}+\dfrac{4}{3}\sqrt{9x+45}=6\)

\(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\)

\(\Leftrightarrow3\sqrt{x+5}=6\)

\(\Leftrightarrow x+5=4\)

hay x=-1

b: Ta có: \(\dfrac{1}{2}\sqrt{x-1}-\dfrac{3}{2}\sqrt{9x-9}+24\sqrt{\dfrac{x-1}{64}}=-17\)

\(\Leftrightarrow\dfrac{1}{2}\sqrt{x-1}-\dfrac{9}{2}\sqrt{x-1}+3\sqrt{x-1}=-17\)

\(\Leftrightarrow\sqrt{x-1}=17\)

\(\Leftrightarrow x-1=289\)

hay x=290

i: =-12*căn 3/2căn 3=-6

h: =72căn 2/12căn 2=6

g: =25căn 12/5căn 6=5căn 2

f: =(15:5)*căn 6:3=3căn 2

d: =-1/2*6*căn 10=-3căn 10

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)

\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)

\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)

\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)

\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)

\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)

\(=\sqrt{5}-2-\sqrt{5}=-2\)

\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)

\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)

\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)

\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)

\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)