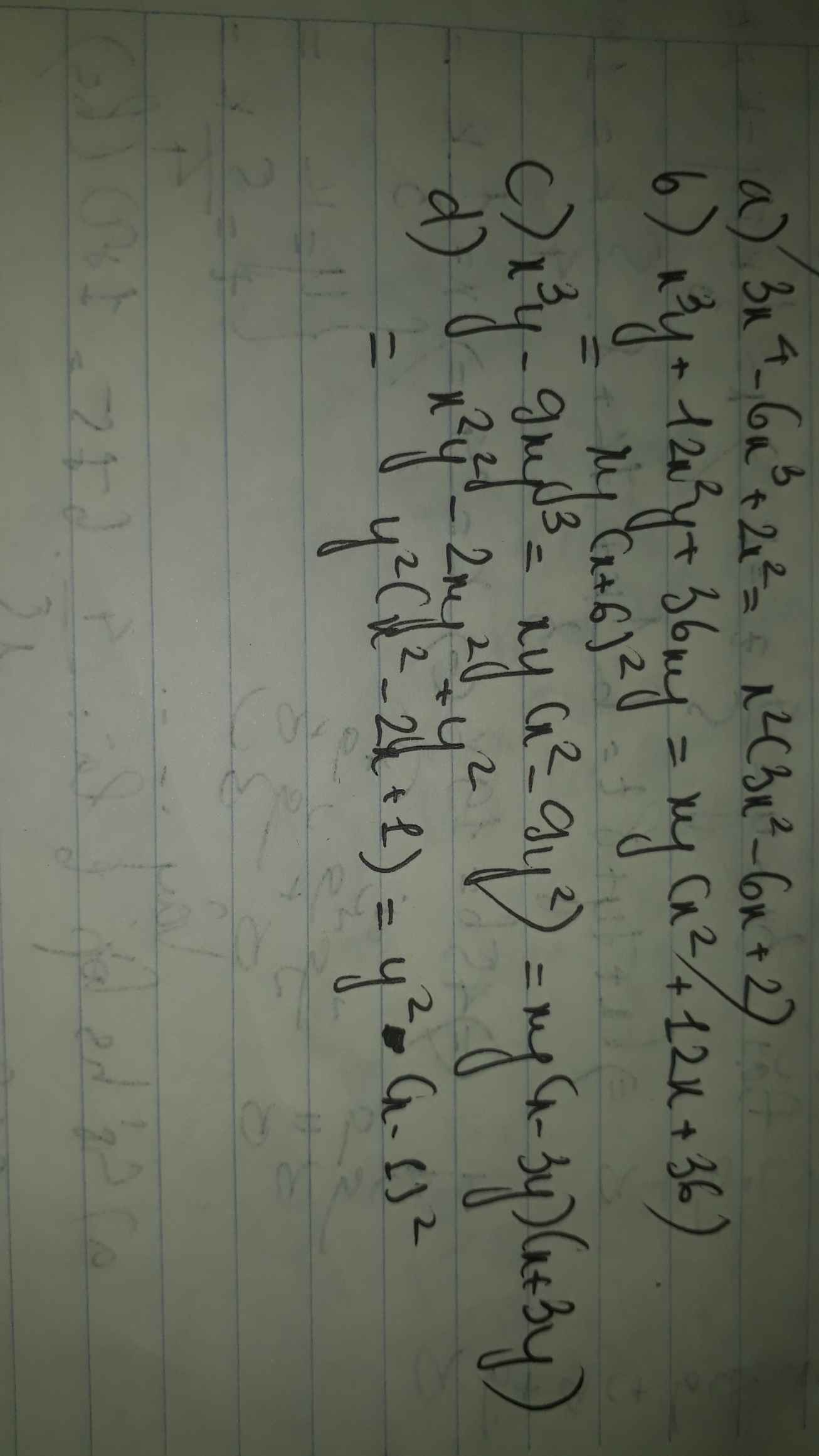2xy+5x2y-x3y

Những câu hỏi liên quan
Bài 4: đặt nhân tử chung
c)x(x-2)+(x-2)2
d) 2x(x-y)2-5(y-x)
Bài 5 :
a) x2-6x-2xy+12y
b) 10ax-5ay-2x+y
c)x4+x3y-x-y
d) x3+2x2-4x-8
e) xy-5x-y2+5y
f) ax-bx-2cx-2a+2b+4c
g) 5x2y+5xy2-b2x-b2y
h) 4x3-4x2-9x+9
Bài 4
c) x(x - 2) + (x - 2)²
= (x - 2)(x + x - 2)
= (x - 2)(2x - 2)
= 2(x - 2)(x - 1)
d) 2x(x - y)² - 5(y - x)
= 2x(x - y)² + 5(x - y)
= (x - y)(2x + 5)
Đúng 1
Bình luận (2)
Bài 5
a) x² - 6x - 2xy + 12y
= (x² - 6x) - (2xy - 12y)
= x(x - 6) - y(x - 6)
= (x - 6)(x - y)
b) 10ax - 5ay - 2x + y
= (10ax - 5ay) - (2x - y)
= 5a(2x - y) - (2x - y)
= (2x - y)(5a - 1)
c) x⁴ + x³y - x - y
= (x⁴ + x³y) - (x + y)
= x³(x + y) - (x + y)
= (x + y)(x³ - 1)
= (x + y)(x - 1)(x² + x + 1)
d) x³ + 2x² - 4x - 8
= (x³ + 2x²) - (4x + 8)
= x²(x + 2) - 4(x + 2)
= (x + 2)(x² - 4)
= (x + 2)(x + 2)(x - 2)
= (x + 2)²(x - 2)
e) xy - 5x - y² + 5y
= (xy - 5x) - (y² - 5y)
= x(y - 5) - y(y - 5)
= (y - 5)(x - y)
f) ax - bx - 2cx - 2a + 2b + 4c
= (ax - bx - 2cx) - (2a - 2b - 4c)
= x(a - b - 2c) - 2(a - b - 2c)
= (a - b - 2c)(x - 2)
g) 5x²y + 5xy² - b²x - b²y
= (5x²y + 5xy²) - (b²x + b²y)
= 5xy(x + y) - b²(x + y)
= (x + y)(5xy - b²)
h) 4x³ - 4x² - 9x + 9
= (4x³ - 4x²) - (9x - 9)
= 4x²(x - 1) - 9(x - 1)
= (x - 1)(4x² - 9)
= (x - 1)(2x - 3)(2x + 3)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử a) 3x4 - 6x3 + 2x2 e) x2 + 6x + 9 - y2b) x3y + 12x2y + 36xy f) x2 - 2xy + 7x - 14c) x3y - 9xy3 g) x2y - 3xy2 - 2xy + 6y2d) x2y2 - 2xy2 + y2 h) 5x2 - 10xy + 5y2 - 20Làm giúp mình với mình đang cần gấp
Đọc tiếp
Phân tích đa thức thành nhân tử
a) 3x4 - 6x3 + 2x2 e) x2 + 6x + 9 - y2
b) x3y + 12x2y + 36xy f) x2 - 2xy + 7x - 14
c) x3y - 9xy3 g) x2y - 3xy2 - 2xy + 6y2
d) x2y2 - 2xy2 + y2 h) 5x2 - 10xy + 5y2 - 20
Làm giúp mình với mình đang cần gấp
e: \(x^2+6x+9-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+3-y\right)\left(x+3+y\right)\)
f: \(x^2-2x+7x-14\)
\(=x\left(x-2\right)+7\left(x-2\right)\)
=(x-2)(x+7)
h: \(5x^2-10xy+5y^2-20\)
\(=5\left(x^2-2xy+y^2-4\right)\)
\(=5\left(x-y-2\right)\left(x-y+2\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử a) 3x4 - 6x3 + 2x2 e) x2 + 6x + 9 - y2b) x3y + 12x2y + 36xy f) x2 - 2xy + 7x - 14c) x3y - 9xy3 g) x2y - 3xy2 - 2xy + 6y2d) x2y2 - 2xy2 + y2 h) 5x2 - 10xy + 5y2 - 20Làm giúp mình với mình đang cần gấp
Đọc tiếp
Phân tích đa thức thành nhân tử
a) 3x4 - 6x3 + 2x2 e) x2 + 6x + 9 - y2
b) x3y + 12x2y + 36xy f) x2 - 2xy + 7x - 14
c) x3y - 9xy3 g) x2y - 3xy2 - 2xy + 6y2
d) x2y2 - 2xy2 + y2 h) 5x2 - 10xy + 5y2 - 20
Làm giúp mình với mình đang cần gấp
a: \(3x^4-6x^3+2x^2=x^2\left(3x^2-6x+2\right)\)
b: \(x^3y+12x^2y+36xy=xy\left(x^2+12x+36\right)=xy\left(x+6\right)^2\)
c: \(x^3y-9xy^3=xy\left(x^2-9y^2\right)=xy\left(x-3y\right)\left(x+3y\right)\)
d: \(x^2y^2-2xy^2+y^2=y^2\left(x-1\right)^2\)
Đúng 0
Bình luận (1)
Cho đa thức
A = 5x2y- 3xy+ x4y2- 5x2y+ 2xy+ x2+ xy+ 1
a, Thu gọn rồi tính giá trị của đa thức A tại x= -1; y= 1
b, Chứng tỏ rằng đa thức A luôn nhận giá trị dương với mọi giá trị của x, y
a: A=5x^2y-5x^2y-3xy+2xy+xy+x^4y^2+1+x^2
=x^4y^2+x^2+1
Khi x=-1 và y=1 thì A=(-1)^4*1^2+(-1)^2+1=3
b: A=x^2(x^2y^2+1)+1>=1>0 với mọi x,y
=>A luôn dương với mọi x,y
Đúng 0
Bình luận (0)
Tính giá trị mỗi biểu thức sau tại x = 1; y = -1 và z = -2:
2xy(5x2y + 3x – z)
Thay x =1 ; y = –1 và z = –2 vào biểu thức ta được
2xy (5x2y + 3x – z)
= 2.1(–1).[5.12.( –1) + 3.1 – (–2)]
= – 2.[5.1.( –1) + 3 + 2]
= –2. (–5 + 3 + 2)
= –2.0
= 0
Vậy đa thức có giá trị bằng 0 tại x =1; y = –1 và z = –2.
Đúng 0
Bình luận (0)
Câu 1: Biểu thức nào là đơn thức? A. 5x2y B. 2xy+1 C. 3x-2 D. 2x2+7
Đọc tiếp
Câu 1: Biểu thức nào là đơn thức?
A. 5x2y B. 2xy+1 C. 3x-2 D. 2x2+7
Cho hai đa thức sau:
P = −x3y−xy+x2+4x3y+2xy+1−x3y−xy+x2+4x3y+2xy+1
Q = x3y−8xy−5+2x3y+9x2+4−10x2x3y−8xy−5+2x3y+9x2+4−10x2
a) Thu gọn đa thức P và Q. Xác định bậc của đa thức P và Q sau khi thu gọn.
b) Tính A = P + Q và B = P - Q
c) Tính giá trị của đa thức A khi x=1x=1 và y=−1y=−1
: Tính giá trị của các biểu thức sau tại x = l; y = –1; z = –2.
a) 2xy (5x2y + 3x – z);
b) xy2 +y2z3 + z3x4
a: Thay x=1; y=-1 và z=-2 vào biểu thức \(2xy\left(5x^2y+3x-z\right)\), ta được:
\(2\cdot1\cdot\left(-1\right)\cdot\left(-5+3+2\right)\)
=0
b: Thay x=1; y=-1 và z=-2 vào biểu thức \(xy^2+y^2z^3+z^3x^4\), ta được:
\(1\cdot\left(-1\right)^2+\left(-1\right)^2\cdot\left(-8\right)+\left(-8\right)\cdot1\)
\(=1-8-8=-15\)
Đúng 0
Bình luận (0)
cho các đa thức M=4x3-2x2y+xy+1 N=3x2y+2xy-5 P=4x3-5x2y+3xy+1 Tính M-N-P:P-N-M
M-N-P=4x3-2x2y+xy+1-3x2y-2xy+5-4x3+5x2y-3xy-1
=-4xy+5
p-n-m=4x3-5x2y+3x2y+1-3x2y-2xy+5-4x3+2x2y-xy-1
=-6x2y+5
Đúng 1
Bình luận (0)