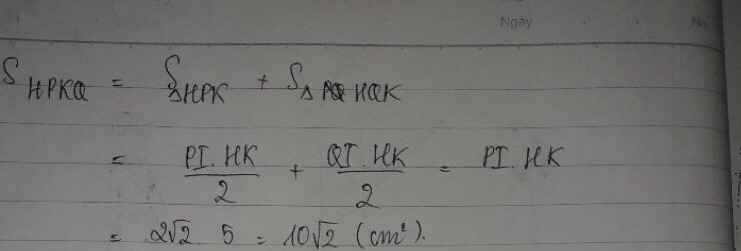vẽ 3 vị trí tương đối của đường thẳng và đường tròn. kẻ OH vuông góc với a so sánh OH và bán kính

Những câu hỏi liên quan
1.Cho đoạn thẳng HK = 5cm. Vẽ đường tròn tâm H, bán kính 2cm và đường tròn tâm K, bản kính 3cm.
a) Xác định vị trí tương đối của hai đường tròn trên.
b) Trên đoạn thẳng HK lấy điểm D sao cho IK = 1cm. Vẽ đường thẳng đi qua I và vuông góc với HK, đường thẳng này cắt đường tròn (K) tại hai điểm P, Q. Tính diện tích tứ giác HPKQ.
Cho hình vuông ABCD, Trên đường chéo BD lấy BH = BA. Qua H kẽ đường thẳng vuông góc với BD và đường vuông góc cắt AD tại O
a) So sánh: OA, OH, HD
b) Xác định vị trí tương đối của đường thẳng BD với vòng ( O; A)
Cho tam giác ABC vuông tại A ( AB < AC ). Vẽ đường tròn tâm O đường kính BC
a. Xác định vị trí tương đối của điểm A với đường tròn (O)
b. Tiếp tuyến tại A và B của đường tròn O cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt AD tại E, cắt AC tại I. Xác định vị trí tương đối của EC với đường tròn O
c. CM rằng: EC2 = EA.ED - OI.OE
Cho tam giác ABC vuông tại A ( AB < AC ). Vẽ đường tròn tâm O đường kính BC
a. Xác định vị trí tương đối của điểm A với đường tròn (O)
b. Tiếp tuyến tại A và B của đường tròn O cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt AD tại E, cắt AC tại I. Xác định vị trí tương đối của EC với đường tròn O
c. CM rằng: EC2 = EA.ED - OI.OE
a: Vì ΔABC vuông tại A
nên A nằm trên (O)
b: ΔOAC cân tại O
mà OI là đường cao
nên OI là phân giác của gócc AOC
Xét ΔOAE và ΔOCE có
OA=OC
góc AOE=góc COE
OE chung
Do đó: ΔOAE=ΔOCE
=>góc OCE=90 độ
=>EC là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R và đường thẳng d cố định không cắt đường tròn . Từ điểm A bất kì trên đường thẳng d kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm) . Từ B kẻ đường thẳng vuông góc với OH tại H , trên tia đối của tia HB lấy điểm C sao cho HCHB.A,Chứng minh điểm C thuộc (O;R) và AC là tiếp tuyến của đường tròn (O)B,Từ O kẻ đường thẳng vuông góc với đường thẳng d tại I , OI cắt BC tại IC. Chứng minh OH.OAOI.OKR^2
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng d cố định không cắt đường tròn . Từ điểm A bất kì trên đường thẳng d kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm) . Từ B kẻ đường thẳng vuông góc với OH tại H , trên tia đối của tia HB lấy điểm C sao cho HC=HB.
A,Chứng minh điểm C thuộc (O;R) và AC là tiếp tuyến của đường tròn (O)
B,Từ O kẻ đường thẳng vuông góc với đường thẳng d tại I , OI cắt BC tại IC. Chứng minh OH.OA=OI.OK=R^2
Bài 1.21 Cho đường tròn tâm O đường kính AB. Kẻ lần lượt các đường thẳng d1,d2 vuông góc với AB tại A và tại B. Trên đường thẳng d1 lấy điểm C khác A. Đường thẳng vuông góc với CO tại O cắt đường thẳng d2 tại D.a. Xét vị trí tương đối của đường thẳng CD với đường tròn (O).b. Điểm C ở vị trí nào trên d1 thì tổng AC + BD nhỏ nhất.c. Cho AB 2a. Tính tích AC · BD theo a.
Đọc tiếp
Bài 1.21 Cho đường tròn tâm O đường kính AB. Kẻ lần lượt các đường thẳng d1,d2 vuông góc với AB tại A và tại B. Trên đường thẳng d1 lấy điểm C khác A. Đường thẳng vuông góc với CO tại O cắt đường thẳng d2 tại D.
a. Xét vị trí tương đối của đường thẳng CD với đường tròn (O).
b. Điểm C ở vị trí nào trên d1 thì tổng AC + BD nhỏ nhất.
c. Cho AB = 2a. Tính tích AC · BD theo a.
Cho đường tròn (O) đường kính AB , điểm C nằm giữa A và O . Vẽ đường tròn (I) có đường kính CBa) Xét vị trí tương đối của 2 đường tròn (O) và (I)b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC . Tứ giác ADCE là hình gì ? Vì sao ?c) Gọi K là giao điểm của DB là đường tròn (I) . Chứng minh rằng 3 điểm E,C,K thẳng hàngd) Chứng minh rằng HK là tiếp tuyến của đường tròn (I)*******BÀI NÀY VẼ HÌNH HƠI KHÓ NÊN CẦN CẢ HÌNH********
Đọc tiếp
Cho đường tròn (O) đường kính AB , điểm C nằm giữa A và O . Vẽ đường tròn (I) có đường kính CB
a) Xét vị trí tương đối của 2 đường tròn (O) và (I)
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC . Tứ giác ADCE là hình gì ? Vì sao ?
c) Gọi K là giao điểm của DB là đường tròn (I) . Chứng minh rằng 3 điểm E,C,K thẳng hàng
d) Chứng minh rằng HK là tiếp tuyến của đường tròn (I)
*******BÀI NÀY VẼ HÌNH HƠI KHÓ NÊN CẦN CẢ HÌNH********
a: OI+IB=OB
=>OI=OB-IB
=>\(OI=R-r\)
=>Hai đường tròn (O) và (I) tiếp xúc trong với nhau tại B
b: Ta có: ΔODE cân tại O
mà OH là đường cao
nên H là trung điểm của DE
Xét tứ giác ADCE có
H là trung điểm chung của AC và DE
=>ADCE là hình bình hành
Hình bình hành ADCE có AC\(\perp\)DE
nên ADCE là hình thoi
c: Xét (I) có
ΔCKB nội tiếp
CB là đường kính
Do đó: ΔCKB vuông tại K
=>CK\(\perp\)KB tại K
=>CK\(\perp\)DB tại K
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)BE tại E
Ta có: ADCE là hình thoi
=>AE//CD
mà AE\(\perp\)EB
nên CD\(\perp\)EB
Xét ΔDEB có
BH,DC là các đường cao
BH cắt DC tại C
Do đó: C là trực tâm của ΔDEB
=>EC\(\perp\)DB
mà CK\(\perp\)DB
và EC,CK có điểm chung là C
nên E,C,K thẳng hàng
d:
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét tứ giác DHCK có \(\widehat{DHC}+\widehat{DKC}=90^0+90^0=180^0\)
nên DHCK là tứ giác nội tiếp
=>\(\widehat{HKC}=\widehat{HDC}\)
mà \(\widehat{HDC}=\widehat{ADH}\)(DH là phân giác của góc ADC do ADCE là hình thoi)
nên \(\widehat{HKC}=\widehat{ADH}\)
mà \(\widehat{ADH}=\widehat{ABD}\left(=90^0-\widehat{DAB}\right)\)
nên \(\widehat{HKC}=\widehat{ABD}\)
Ta có: IC=IK
=>ΔICK cân tại I
=>\(\widehat{ICK}=\widehat{IKC}\)
\(\widehat{HKI}=\widehat{HKC}+\widehat{IKC}\)
\(=\widehat{ABD}+\widehat{ICK}\)
\(=\widehat{KBC}+\widehat{KCB}=90^0\)
=>HK\(\perp\)KI tại K
=>HK là tiếp tuyến tại K của (I)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=3cm, AC=4cm. Vẽ đường tròn tâm A bán kính 2,8cm. Hãy xác định vị trí tương đối của đường thẳng BC và đường tròn (A;2,8)
cho đường tròn tâm O bán kính R đường kính AB. Vẽ điểm C thuộc đường tròn tâm O bán kính R sao cho AC bằng R .kẻ OH vuông góc với AC tại H . qua điểm C vẽ một tiếp tuyến của đường tròn tâm O bán kính R tiếp tuyến này cắt đường thẳng OH tại D Câu a/ chứng minh AD là tiếp tuyến của đường tròn tâm O bán kính R Câu b/ tính BC theo R và tỉ số lượng giác của góc ABCCau c/ gọi M là điểm thuộc tia đối của tia CA . chứng minh MC nhân với MA bằng MO bình phương trừ AO bình phương
Đọc tiếp
cho đường tròn tâm O bán kính R đường kính AB. Vẽ điểm C thuộc đường tròn tâm O bán kính R sao cho AC bằng R .kẻ OH vuông góc với AC tại H . qua điểm C vẽ một tiếp tuyến của đường tròn tâm O bán kính R tiếp tuyến này cắt đường thẳng OH tại D
Câu a/ chứng minh AD là tiếp tuyến của đường tròn tâm O bán kính R
Câu b/ tính BC theo R và tỉ số lượng giác của góc ABC
Cau c/ gọi M là điểm thuộc tia đối của tia CA . chứng minh MC nhân với MA bằng MO bình phương trừ AO bình phương