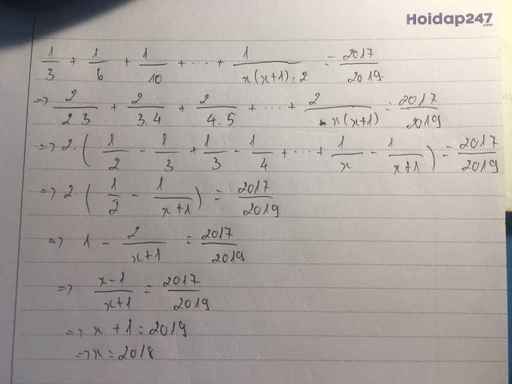\(\dfrac{1}{3}\)+\(\dfrac{1}{6}\)+\(\dfrac{1}{10}\)+.....+1/xx(x+1):2

Những câu hỏi liên quan
Tìm x:
\(\dfrac{1}{3}\) + \(\dfrac{1}{6}\)+ \(\dfrac{1}{10}\)+ ...+ \(\dfrac{1}{xx\left(x+1\right):2}\)= \(\dfrac{2017}{2019}\)
Mọ người giúp em với ạ! Em cảm ơn!
mn ghi giúp em chi tiết bài giải nx ạ!
Đúng 0
Bình luận (0)
Tính:
a) (6 : dfrac{3}{5} 1dfrac{1}{6} x dfrac{6}{7} ) : ( 4dfrac{1}{5} x dfrac{10}{11} + 5dfrac{2}{11} )
b) (1-dfrac{1}{2}) x (1-dfrac{1}{3}) x (1-dfrac{1}{4}) x ..... x (1-dfrac{1}{2003}) x (1-dfrac{1}{2007})
Đọc tiếp
Tính:
a) (6 : \(\dfrac{3}{5}\) \(1\dfrac{1}{6}\) x \(\dfrac{6}{7}\) ) : ( \(4\dfrac{1}{5}\) x \(\dfrac{10}{11}\) + \(5\dfrac{2}{11}\) )
b) (\(1-\dfrac{1}{2}\)) x (\(1-\dfrac{1}{3}\)) x (\(1-\dfrac{1}{4}\)) x ..... x (\(1-\dfrac{1}{2003}\)) x (\(1-\dfrac{1}{2007}\))
1/ \(\dfrac{5x+1}{8}-\dfrac{x-2}{4}=\dfrac{1}{2}\)
2/ \(\dfrac{x+3}{4}+\dfrac{1-3x}{3}=\dfrac{-x+1}{18}\)
3/ \(\dfrac{x+2}{4}-\dfrac{5x}{6}=\dfrac{1-x}{3}\)
4/ \(\dfrac{x-3}{2}-\dfrac{x+1}{10}=\dfrac{x-2}{5}\)
5/ \(\dfrac{4x+1}{4}-\dfrac{9x-5}{12}+\dfrac{x-2}{3}=0\)
1: Ta có: \(\dfrac{5x+1}{8}-\dfrac{x-2}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow5x+1-2\left(x-2\right)=4\)
\(\Leftrightarrow5x+1-2x+4=4\)
\(\Leftrightarrow3x=-1\)
hay \(x=-\dfrac{1}{3}\)
2: Ta có: \(\dfrac{x+3}{4}+\dfrac{1-3x}{3}=\dfrac{-x+1}{18}\)
\(\Leftrightarrow9x+27+12-36x=-2x+2\)
\(\Leftrightarrow-27x+2x=2-39\)
hay \(x=\dfrac{37}{25}\)
3: Ta có: \(\dfrac{x+2}{4}-\dfrac{5x}{6}=\dfrac{1-x}{3}\)
\(\Leftrightarrow3x+6-10x=4-4x\)
\(\Leftrightarrow-7x+4x=4-6=-2\)
hay \(x=\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
4: Ta có: \(\dfrac{x-3}{2}-\dfrac{x+1}{10}=\dfrac{x-2}{5}\)
\(\Leftrightarrow5x-15-x-1=2x-4\)
\(\Leftrightarrow4x-2x=-4+16=12\)
hay x=6
5: Ta có: \(\dfrac{4x+1}{4}-\dfrac{9x-5}{12}+\dfrac{x-2}{3}=0\)
\(\Leftrightarrow12x+3-9x+5+4x-8=0\)
\(\Leftrightarrow7x=0\)
hay x=0
Đúng 0
Bình luận (0)
1,dfrac{3}{16}- ( x - dfrac{5}{4} ) - ( dfrac{3}{4} + dfrac{-7}{8} - 1 ) 2dfrac{1}{2}
2,dfrac{1}{2} . ( dfrac{1}{6} - dfrac{9}{10} ) dfrac{1}{5} - x + ( dfrac{1}{15} - dfrac{-1}{5} )
Giúp mik nhanh với ạ .
Đọc tiếp
1,\(\dfrac{3}{16}\)- ( x - \(\dfrac{5}{4}\) ) - ( \(\dfrac{3}{4}\) + \(\dfrac{-7}{8}\) - 1 ) = \(2\dfrac{1}{2}\)
2,\(\dfrac{1}{2}\) . ( \(\dfrac{1}{6}\) - \(\dfrac{9}{10}\) ) = \(\dfrac{1}{5}\) - x + ( \(\dfrac{1}{15}\) - \(\dfrac{-1}{5}\) )
Giúp mik nhanh với ạ .
\(\dfrac{3}{16}\) - (\(x\) - \(\dfrac{5}{4}\)) - ( \(\dfrac{3}{4}\) - \(\dfrac{7}{8}\) - 1) = 2\(\dfrac{1}{2}\)
\(\dfrac{3}{16}\) - \(x\) + \(\dfrac{5}{4}\) - \(\dfrac{3}{4}\) + \(\dfrac{7}{8}\) + 1 = \(\dfrac{5}{2}\)
\(\dfrac{3}{16}\) - \(x\) + ( \(\dfrac{5}{4}\) - \(\dfrac{3}{4}\)) + (\(\dfrac{7}{8}\) + 1) = \(\dfrac{5}{2}\)
\(\dfrac{3}{16}\) - \(x\) + \(\dfrac{1}{2}\) + \(\dfrac{15}{8}\) = \(\dfrac{5}{2}\)
( \(\dfrac{3}{16}\) + \(\dfrac{1}{2}\) + \(\dfrac{15}{8}\)) - \(x\) = \(\dfrac{5}{2}\)
\(\dfrac{41}{16}\) - \(x\) = \(\dfrac{5}{2}\)
\(x\) = \(\dfrac{41}{16}\) - \(\dfrac{5}{2}\)
\(x\) = \(\dfrac{1}{16}\)
Đúng 2
Bình luận (0)
2, \(\dfrac{1}{2}\).( \(\dfrac{1}{6}\) - \(\dfrac{9}{10}\)) = \(\dfrac{1}{5}\) - \(x\) + ( \(\dfrac{1}{15}\) - \(\dfrac{-1}{5}\))
\(\dfrac{1}{2}\).(-\(\dfrac{11}{15}\)) = \(\dfrac{1}{5}\) - \(x\) + \(\dfrac{1}{15}\) + \(\dfrac{1}{5}\)
- \(\dfrac{11}{30}\) = ( \(\dfrac{1}{5}\)+ \(\dfrac{1}{5}\)+ \(\dfrac{1}{15}\)) - \(x\)
- \(\dfrac{11}{30}\) = \(\dfrac{7}{15}\) - \(x\)
\(x\) = \(\dfrac{7}{15}\) + \(\dfrac{11}{30}\)
\(x\) = \(\dfrac{5}{6}\)
Đúng 1
Bình luận (0)
Tìm x:a) (2x - 3)(6 - 2x) 0b) 5dfrac{4}{7}:x13 c) 2x - dfrac{3}{7} 6dfrac{2}{7}d) dfrac{x}{5} + dfrac{1}{2} dfrac{6}{10}e) dfrac{x+3}{15}dfrac{1}{3}f) dfrac{x-12}{4}dfrac{1}{2}g) 2dfrac{1}{4}.left(x-7dfrac{1}{3}right)1,5h) left(4,5-2xright).1dfrac{4}{7}dfrac{11}{14}i) dfrac{2}{3}left(x-25%right)dfrac{1}{6}k) dfrac{3}{2}x-1dfrac{1}{2}x-dfrac{3}{4}
Đọc tiếp
Tìm x:
a) (2x - 3)(6 - 2x) = 0
b) \(5\dfrac{4}{7}:x=13\)
c) 2x - \(\dfrac{3}{7}\) = \(6\dfrac{2}{7}\)
d) \(\dfrac{x}{5}\) + \(\dfrac{1}{2}\) = \(\dfrac{6}{10}\)
e) \(\dfrac{x+3}{15}=\dfrac{1}{3}\)
f) \(\dfrac{x-12}{4}=\dfrac{1}{2}\)
g) \(2\dfrac{1}{4}\).\(\left(x-7\dfrac{1}{3}\right)=1,5\)
h) \(\left(4,5-2x\right).1\dfrac{4}{7}=\dfrac{11}{14}\)
i) \(\dfrac{2}{3}\left(x-25\%\right)=\dfrac{1}{6}\)
k) \(\dfrac{3}{2}x-1\dfrac{1}{2}=x-\dfrac{3}{4}\)
a) (2x - 3)(6 - 2x) = 0
=> \(\left[{}\begin{matrix}2x-3=0\\6-2x=0\end{matrix}\right.=>\left[{}\begin{matrix}2x=3\\2x=6\end{matrix}\right.=>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=3\end{matrix}\right.\)
b) \(5\dfrac{4}{7}:x=13=>\dfrac{39}{7}:x=13=>x=\dfrac{39}{7}:13=>x=\dfrac{3}{7}\)
c) \(2x-\dfrac{3}{7}=6\dfrac{2}{7}=>2x-\dfrac{3}{7}=\dfrac{44}{7}=>2x=\dfrac{47}{7}=>x=\dfrac{47}{14}\)
d) \(\dfrac{x}{5}+\dfrac{1}{2}=\dfrac{6}{10}=>\dfrac{x}{5}=\dfrac{6}{10}-\dfrac{1}{2}=>\dfrac{x}{5}=\dfrac{1}{10}=>x.10=5=>x=\dfrac{1}{2}\)
e) \(\dfrac{x+3}{15}=\dfrac{1}{3}=>\left(x+3\right).3=15=>x+3=5=>x=2\)
Đúng 3
Bình luận (0)
f)\(\dfrac{x-12}{4}=\dfrac{1}{2}=\dfrac{x-12}{4}=\dfrac{2}{4}\)
⇒\(x-12=2\)
\(x=2+12\)
x = 14
g)2\(\dfrac{1}{4}.\left(x-7\dfrac{1}{3}\right)=1,5\)
\(\dfrac{9}{4}.\left(x-\dfrac{22}{3}\right)=1,5\)
\(\left(x-\dfrac{22}{3}\right)=\dfrac{3}{2}:\dfrac{9}{4}\)
\(x-\dfrac{22}{3}=\dfrac{2}{3}\)
\(x=\dfrac{2}{3}+\dfrac{22}{3}\)
\(x=8\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1,dfrac{3}{16}- ( x - dfrac{5}{4} ) - ( dfrac{3}{4} + dfrac{-7}{8} - 1 ) 2dfrac{1}{2}2,dfrac{1}{2} . ( dfrac{1}{6} - dfrac{9}{10} ) dfrac{1}{5} - x + ( dfrac{1}{15} - dfrac{-1}{5} )Giúp mik nhanh với ạ
Đọc tiếp
1,\(\dfrac{3}{16}\)- ( x - \(\dfrac{5}{4}\) ) - ( \(\dfrac{3}{4}\) + \(\dfrac{-7}{8}\) - 1 ) = \(2\dfrac{1}{2}\)
2,\(\dfrac{1}{2}\) . ( \(\dfrac{1}{6}\) - \(\dfrac{9}{10}\) ) = \(\dfrac{1}{5}\) - x + ( \(\dfrac{1}{15}\) - \(\dfrac{-1}{5}\) )
Giúp mik nhanh với ạ
`@` `\text {Ans}`
`\downarrow`
`1,`
`3/16 - (x - 5/4) - (3/4 + (-7)/8 - 1) = 2 1/2`
`=> 3/16 - x + 5/4 - (-1/8 - 1) = 2 1/2`
`=> 3/16 - x + 5/4 - (-9/8) = 2 1/2`
`=> 3/16 - x + 19/8 = 2 1/2`
`=> 3/16 - x = 2 1/2 - 19/8`
`=> 3/16 - x =1/8`
`=> x = 3/16 - 1/8`
`=> x = 1/16`
Vậy, `x = 1/16`
`2,`
`1/2* (1/6 - 9/10) = 1/5 - x + (1/15 - (-1)/5)`
`=> 1/2 * (-11/15) = 1/5 - x + 4/15`
`=> -11/30 = x + 1/5 - 4/15`
`=> x + (-1/15) = -11/30`
`=> x = -11/30 + 1/15`
`=> x = -3/10`
Vậy, `x = -3/10.`
Đúng 2
Bình luận (1)
1 + \(\dfrac{1}{3}\) +\(\dfrac{1}{6}\)+\(\dfrac{1}{10}\) +......+
\(\dfrac{2}{x(x+1)}\) =1\(\dfrac{1989}{1991}\)
\(\dfrac{help}{me}\)
\(1+\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{2}{x\left(x+1\right)}=1\dfrac{1989}{1991}\)
\(\Rightarrow2\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{3980}{1991}\)
\(\Rightarrow2\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{3980}{1991}\)
\(\Rightarrow2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\right)=\dfrac{3980}{1991}\)
\(\Rightarrow2\left(1-\dfrac{1}{x+1}\right)=\dfrac{3980}{1991}\)
\(\Rightarrow1-\dfrac{1}{x+1}=\dfrac{3980}{1991}.\dfrac{1}{2}\)
\(\Rightarrow1-\dfrac{1}{x+1}=\dfrac{1990}{1991}\)
\(\Rightarrow\dfrac{1}{x+1}=1-\dfrac{1990}{1991}\)
\(\Rightarrow\dfrac{1}{x+1}=\dfrac{1}{1991}\)
\(\Rightarrow x+1=1991\)
\(\Rightarrow x=1990\)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Tìm số nguyên x, biết:a)dfrac{6}{x-3} dfrac{2}{3}b) dfrac{14}{13} dfrac{-28}{10-x}c) dfrac{1}{5} dfrac{x:4-1}{10}d) dfrac{x}{4} dfrac{1}{x}e) dfrac{x-2}{50} dfrac{2}{x-2}giúp ưm
Đọc tiếp
Bài 1: Tìm số nguyên x, biết:
a)\(\dfrac{6}{x-3}\) = \(\dfrac{2}{3}\)
b) \(\dfrac{14}{13}\) = \(\dfrac{-28}{10-x}\)
c) \(\dfrac{1}{5}\) = \(\dfrac{x:4-1}{10}\)
d) \(\dfrac{x}{4}\)= \(\dfrac{1}{x}\)
e) \(\dfrac{x-2}{50}\) = \(\dfrac{2}{x-2}\)
giúp ưm
a: =>x-3=9
=>x=12
b: =>10-x=-26
=>x=36
c: =>x:4-1=2
=>x:4=3
=>x=12
d: =>x^2=4
=>x=2 hoặc x=-2
e: =>(x-2)^2=100
=>x-2=10 hoặc x-2=-10
=>x=12 hoặc x=-8
Đúng 0
Bình luận (0)
Tìm x biết:a,dfrac{4}{5}+xdfrac{2}{3}b,dfrac{-5}{6}-xdfrac{2}{3}c,dfrac{1}{2}x+dfrac{3}{4}dfrac{-3}{10}d,dfrac{x}{3}-dfrac{1}{2}dfrac{1}{5}e,dfrac{x+3}{15}dfrac{1}{3}h,x+30%x-1,3k,3dfrac{1}{3}x+16dfrac{1}{4}13,25m,dfrac{x-6}{2}dfrac{50}{x-6}n,x-13,424,5-6,7.5,2p,15,7x+3,6x-96,5q,2,5x-11,6-59,1
Đọc tiếp
Tìm x biết:
\(a,\dfrac{4}{5}+x=\dfrac{2}{3}\)
\(b,\dfrac{-5}{6}-x=\dfrac{2}{3}\)
\(c,\dfrac{1}{2}x+\dfrac{3}{4}=\dfrac{-3}{10}\)
\(d,\dfrac{x}{3}-\dfrac{1}{2}=\dfrac{1}{5}\)
\(e,\dfrac{x+3}{15}=\dfrac{1}{3}\)
\(h,x+30\%x=-1,3\)
\(k,3\dfrac{1}{3}x+16\dfrac{1}{4}=13,25\)
\(m,\dfrac{x-6}{2}=\dfrac{50}{x-6}\)
\(n,x-13,4=24,5-6,7.5,2\)
\(p,15,7x+3,6x=-96,5\)
\(q,2,5x-11,6=-59,1\)
a)4/5+x=2/3
x=2/3-4/5
x=-2/15
b)-5/6-x=2/3
x=-5/6-2/3
x=-3/2
c)1/2x+3/4=-3/10
1/2x=-3/10-3/4
1/2x=-21/20
x=-21/20:1/2
x=-21/10
d)x/3-1/2=1/5
x/3=1/5+1/2
x/3=7/10
10x/30=21/30
10x=21
x=21:10
x=21/10
Đúng 1
Bình luận (0)