giải hệ phương trình 2x+y=4 x+2y=5

Những câu hỏi liên quan
Giải hệ phương trình:
\(\left\{{}\begin{matrix}x^5=x^4-2x^2y+2\\y^5=y^4-2y^2z+2\\z^5=z^4-2z^2x+2\end{matrix}\right.\)
Biểu diễn miễn nghiệm của hệ phương trình:-2x+y=2; -x+2y=4; x+y=5 giải thích và vẽ miền nghiệm
giải hệ phương trình
{-2x-2y=5
{x-y=6
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y=5\\2x-2y=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4y=17\\x-y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{17}{4}\\x=6+y=\dfrac{-17}{4}+6=\dfrac{7}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
\(\left\{{}\begin{matrix}-2x-2y=5\\x-y=6\end{matrix}\right.\)(1)
(1) \(\Rightarrow\)\(\left\{{}\begin{matrix}-2x-2y=5\\2x-2y=12\end{matrix}\right.\)
cộng từng vế của 2 phương trình ta đc:
(1) \(\Rightarrow\)-4y=17
(1)\(\Rightarrow\)\(\left\{{}\begin{matrix}-4y=17\\x-y=6\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}y=\dfrac{-17}{4}\\x+\dfrac{17}{4}=6\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}y=\dfrac{-17}{4}\\x=6-\dfrac{17}{4}\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}y=\dfrac{-17}{4}\\x=\dfrac{7}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a, giải phương trình : 4x²+√2x+3=8x+1
B, giải hệ phương trình :
{√x+y+1+(x+2y)=4(x+y) ²+√3*√x+y
X-4y-3=(2y)²-√2-x²
1) {x^2+2x^2=3 {2x^2+3x^2=5 2) giải theo m {x+y=2m+1 {x-y=1 3)giải theo m {x +2y=3m+2 {2x+y=3m+2 4) cho hệ. {x+3y=4m+4 {2x+y=3m+3 Tìm m để hệ có nghiệm (x,y) thỏa mãn x+y=4 HỆ PHƯƠNG TRÌNH HẾT Ạ Giúp mik với nhé
4:
x+3y=4m+4 và 2x+y=3m+3
=>2x+6y=8m+8 và 2x+y=3m+3
=>5y=5m+5 và x+3y=4m+4
=>y=m+1 và x=4m+4-3m-3=m+1
x+y=4
=>m+1+m+1=4
=>2m+2=4
=>2m=2
=>m=1
3:
x+2y=3m+2 và 2x+y=3m+2
=>2x+4y=6m+4 và 2x+y=3m+2
=>3y=3m+2 và x+2y=3m+2
=>y=m+2/3 và x=3m+2-2m-4/3=m+2/3
Đúng 0
Bình luận (0)
Giải các hệ phương trình:
5
+
2
x
+
y
3
-
5
-...
Đọc tiếp
Giải các hệ phương trình: 5 + 2 x + y = 3 - 5 - x + 2 y = 6 - 2 5
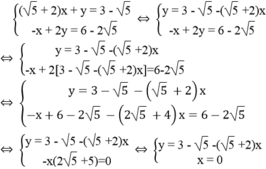
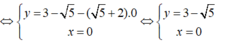
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (0; 3 - 5 ).
Đúng 0
Bình luận (0)
Giải hệ phương trình :
x+2y=5 và 2x-3y=-4
Có: \(\left\{{}\begin{matrix}x+2y=5\\2x-3y=-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x+4y=10\left(1\right)\\2x-3y=-4\left(2\right)\end{matrix}\right.\)
Lấy (1) trừ (2) vế theo vế, ta có: 7y=14 hay y=2 \(\Rightarrow x=1\)
Vậy nghiệm của hệ phương trình là (1;2)
Đúng 4
Bình luận (0)
\(\left\{{}\begin{matrix}x+2y=5\\2x-3y=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+6y=15\\4x-6y=-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=7\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\1+2y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Đúng 3
Bình luận (0)
`{(x + 2y = 5),(2x - 3y = -4):}`
`<=>{(2x + 4y = 10),(2x - 3y = -4):}`
`<=>{(7y = 14),(x + 2y = 5):}`
`<=>{(y = 2),(x + 2 . 2 = 5):}`
`<=>{(x = 1),(y = 2):}`
Vậy hệ ptr có nghiệm `(x ; y) = ( 1; 2)`
Đúng 3
Bình luận (0)
giải các hệ phương trình
9x-6y=4 và 3(4x-3y)=-3x+y+7
3(x+1)+2y=-x và 5(x+y)=-3x+y-5
2(2x+3y)=3(2x-3y)+10 và 4x-3y=4(6y-2x)+3
giải các hệ phương trình sau
a.{ x + 3y = -2
{ 5x - 4y = 11
b.{ 3xy = 5
{ 5x + 2y = 23
c.{ 3x +5y = 1
{ 2x - y = -8
d.{ x - 2y + 6 = 0
{ 5x - 3y - 5 = 0
e.{ 2(x + y) + 3(x - y) = 4
{ (x + y) + 2(x - y) = 5
\(a,\Leftrightarrow\left\{{}\begin{matrix}5x+15y=-10\\5x-4y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19y=-21\\5x-4y=11\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{21}{19}\\5x-4\left(-\dfrac{21}{19}\right)=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25}{19}\\y=-\dfrac{21}{19}\end{matrix}\right.\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\10x-5y=-40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\13x=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=2\end{matrix}\right.\\ d,\Leftrightarrow\left\{{}\begin{matrix}5x-10y=-30\\5x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-3y=5\\-7y=-35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\\ e,\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\2\left(x+y\right)+4\left(x-y\right)=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=6\\2\left(x+y\right)+3\cdot6=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=6\\x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{13}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)






















