E= a√a+b√b/√a+√b - √ab

Những câu hỏi liên quan
ab E Q
a-b=2(a+b)=a:b
a+b=ab=a:b
tìm a,b e N* biết a>b , ab = 128 , BCNN ( a,b) = 64
Để tìm a và b, ta cần tìm hai số tự nhiên a và b thỏa mãn các điều kiện đã cho.
Vì ab = 128 và BCNN(a, b) = 64, ta có thể suy ra rằng a và b phải là các ước số của 128 và cùng chia hết cho 64.
Danh sách các ước số của 128 là: 1, 2, 4, 8, 16, 32, 64, 128.
Vì a > b, nên ta có thể thử các cặp ước số (a, b) theo thứ tự giảm dần.
- Nếu a = 128 và b = 32, ta có ab = 128 * 32 = 4096, không thỏa mãn ab = 128.
- Nếu a = 64 và b = 64, ta có ab = 64 * 64 = 4096, không thỏa mãn ab = 128.
- Nếu a = 32 và b = 64, ta có ab = 32 * 64 = 2048, không thỏa mãn ab = 128.
- Nếu a = 16 và b = 64, ta có ab = 16 * 64 = 1024, không thỏa mãn ab = 128.
- Nếu a = 8 và b = 64, ta có ab = 8 * 64 = 512, không thỏa mãn ab = 128.
- Nếu a = 4 và b = 64, ta có ab = 4 * 64 = 256, không thỏa mãn ab = 128.
- Nếu a = 2 và b = 64, ta có ab = 2 * 64 = 128, thỏa mãn ab = 128.
Vậy a = 2 và b = 64 là hai số tự nhiên thỏa mãn a > b, ab = 128 và BCNN(a, b) = 64.
Đúng 0
Bình luận (0)
tìm a,b e N* biết a>b , ab = 128 , BCNN ( a,b) = 64
\(a\cdot b=BCNN\left(a,b\right)\cdotƯCLN\left(a,b\right)\)
=>\(ƯCLN\left(a,b\right)=\dfrac{128}{64}=2\)
=>\(\left\{{}\begin{matrix}a=2k\\b=2e\end{matrix}\right.\)
a>b>0 nên 2k>2e>0
=>k>e>0
\(a\cdot b=128\)
=>\(2k\cdot2e=128\)
=>\(k\cdot e=\dfrac{128}{4}=32\)
mà k>e>0
nên \(\left(k,e\right)\in\left\{\left(32;1\right);\left(16;2\right);\left(8;4\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(64;2\right);\left(16;8\right);\left(32;4\right)\right\}\)
mà BCNN(a,b)=64
nên a=64 và b=2
Đúng 1
Bình luận (0)
Tìm số ab biết :
a) ab : ( a - b ) = 13 ( dư 1)
b) ab : 5 dư 4 và ( ab - 1 ) chia hết cho 9
c) a,b – b,a = *8 và a + b = 8
d) ba – ab = *3 và a + b = 11 -a
e) a + b < 9 và a < b
Tìm a, b (a, b E số nguyên),biêt:
ab+ 12=a+b
cho a-b=7 , ab=60 Tính: a) a+b b)a^3+b^3 c)a^4+b^4 e)a^6+b^6
a, CMR với mọi số nguyên n không chia hết cho 5 thì \(n^4-1\) chia hết cho 5
b, Tìm tất cả các số nguyên tố a, b, c ,d, e tm \(a^4+b^4+c^4+d^4+e^4=abcde\)
c, Tìm các số nguyênduwongc a,b tm \(a\left(ab+1\right)⋮a^2+b\) và \(b\left(ab+1\right)⋮b^2-a\)
Đề HSG Nghệ An ak bạn
P = \(n^4-1=\left(n^2-1\right)\left(n^2+1\right)=\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n^2-4+5\right)=\left(n-2\right)\left(n+2\right)\left(n-1\right)\left(n+1\right)+5\left(n-1\right)\left(n+1\right)\)
P \(⋮5\Leftrightarrow Q=\left(n-2\right)\left(n-1\right)\left(n+1\right)\left(n+2\right)⋮5\)
mà n không chia hết cho 5 => có dạng n = 5k + 1 ;5k + 2 ; 5k + 3 ;5k + 4 (k \(\in Z\))
Khi n = 5k + 1 => n - 1 \(⋮5\Rightarrow Q⋮5\Rightarrow P⋮5\)
tương tự với n = 5k + 2 ; n = 5k + 3 ; n = 5k + 4 thì Q \(⋮5\Rightarrow P⋮5\)
Đúng 0
Bình luận (0)
b.
Điều duy nhất cần chú ý trong bài toán này: \(n^4\equiv1\left(mod5\right)\) với mọi số nguyên n ko chia hết cho 5
Do đó:
- Nếu cả 5 số a;b;c;d;e đều ko chia hết cho 5 thì vế trái chia hết cho 5, vế phải ko chia hết cho 5 (ktm)
- Nếu cả 5 số a;b;c;d;e đều chia hết cho 5 thì do chúng là số nguyên tố
\(\Rightarrow a=b=c=d=e=5\)
Thay vào thỏa mãn
- Nếu có k số (với \(1\le k\le4\)) trong các số a;b;c;d;e chia hết cho 5, thì vế phải chia hết cho 5, vế phải chia 5 dư \(5-k\ne\left\{0;5\right\}\) nên ko chia hết cho 5 \(\Rightarrow\) ktm
Vậy \(\left(a;b;c;d;e\right)=\left(5;5;5;5;5\right)\) là bộ nghiệm nguyên tố duy nhất
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a>0, b>0 ,a≠b
chứng minh ( \(\sqrt{\dfrac{a}{b}}\)-\(\sqrt{\dfrac{b}{a}}\)) :(a-b) = \(\dfrac{1}{\sqrt{ab}}\)
mn giúp e với ạ
\(VT=\left(\sqrt{\dfrac{a}{b}}-\sqrt{\dfrac{b}{a}}\right):\left(a-b\right)\\ =\left(\dfrac{\sqrt{a}}{\sqrt{b}}-\dfrac{\sqrt{b}}{\sqrt{a}}\right).\dfrac{1}{a-b}\\ =\dfrac{\sqrt{a}.\sqrt{a}-\sqrt{b}.\sqrt{b}}{\sqrt{ab}}.\dfrac{1}{a-b}\\ =\dfrac{\sqrt{a^2}-\sqrt{b^2}}{\sqrt{ab}}.\dfrac{1}{a-b}\\ =\dfrac{a-b}{\sqrt{ab}}.\dfrac{1}{a-b}\\ =\dfrac{1}{\sqrt{ab}}=VP\left(dpcm\right)\)
Đúng 4
Bình luận (0)
\(VT=\dfrac{a-b}{\sqrt{ab}}\cdot\dfrac{1}{a-b}=\dfrac{1}{\sqrt{ab}}=VP\)
Đúng 1
Bình luận (0)
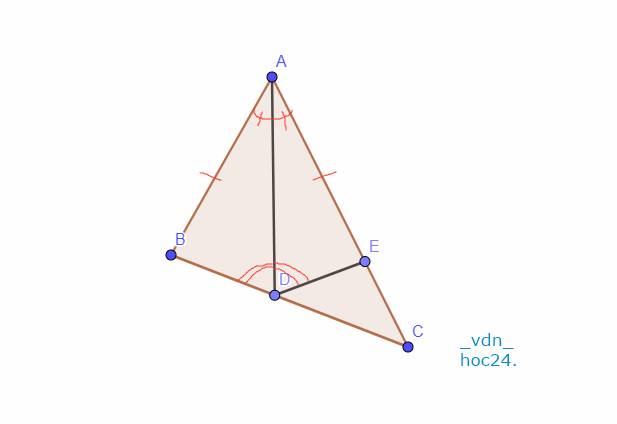
Cho tam giác ABC có AB < AC . Phân giác của góc A cắt cạnh BC tại điểm D. Trên cạnh AC lấy điểm E sao cho AE = AB. Chứng minh
a) ∆ A B D = ∆ A E D .
b) DA là tia phân giác của góc BDE. Từ đó suy ra A B C ^ > A C B ^ .
\(\text{#TNam}\)
`a,` \(\text{Xét Tam giác ABD và Tam giác AED có:}\)
`AB = AE (g``t)`
\(\widehat{BAD}=\widehat{EAD} (\text {tia phân giác} \) \(\widehat{BAE})\)
`\text {AD chung}`
`=> \text {Tam giác ABD = Tam giác AED (c-g-c)}`
`b,`
\(\text{Vì Tam giác ABD = Tam giác AED (a)}\)
`->`\(\widehat{ADB}=\widehat{ADE} (\text {2 góc tương ứng})\)
`-> \text {AD là tia phân giác}` \(\widehat{BDE}\)
\(\text{Xét Tam giác ABC:}\)
`AC > AB (g``t)`
\(\text{Theo định lý của quan hệ giữa góc và cạnh đối diện trong 1 tam giác}\)
`->`\(\widehat{ABC}>\widehat{ACB}.\)
Đúng 3
Bình luận (0)
























